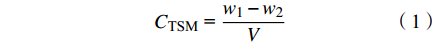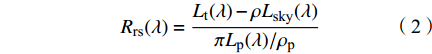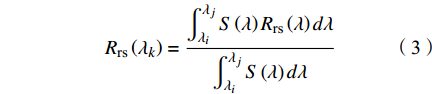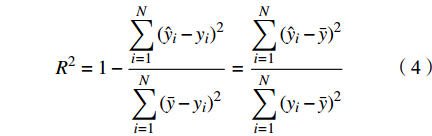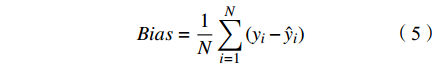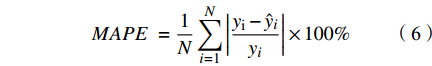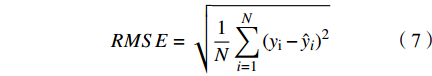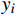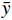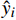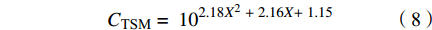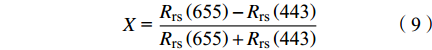Remote sensing estimation of total suspended matter concentration in the mussel culture area
-
摘要:
悬浮颗粒物（total suspended matter, TSM）是重要的水环境参数，影响着海水的透明度和初级生产力，因此总悬浮颗粒物的监测对于海洋牧场环境的评价具有重要意义。卫星遥感技术具有显著的时空观测优势，但目前尚无专门针对海洋牧场小尺度海域的TSM遥感产品。本研究以浙江嵊泗枸杞岛贻贝养殖区为研究对象，基于春、夏、秋、冬4个季节的调查实测数据，建立了面向Landsat-8卫星遥感影像的TSM浓度定量反演模型。验证结果表明，反演模型具有良好的估算精度，决定系数R2为0.72，均方根误差为6.59 g/m3，绝对偏差为0.72 g/m3，平均绝对百分误差为29.8%；进一步将其用于2021－2022年春、夏、秋、冬4个季节的Landsat-8影像，反演了贻贝养殖区及毗邻海域的TSM浓度遥感产品，分析了其时空变化特征。
-
关键词:
- 贻贝养殖区 /
- 悬浮颗粒物浓度 /
- 遥感反演模型 /
- Landsat-8 OLI卫星影像
Abstract:Total suspended matter (TSM) is an important water constituent, influencing seawater’s transparency and primary productivity. Therefore, monitoring TSM concentration is of great significance for evaluating marine ranch environments. Satellite remote sensing has significant advantages in terms of spatial and temporal observations. However, the current TSM product of ocean color remote sensing is for large-scale regions, lacking specific products for small-scale regions, like the marine ranch. In this study, we focused on the mussel culture area around Gouqi island in Shengsi, Zhejiang province, and conducted four observation cruises during different seasons. Based on the in situ data, we proposed a remote sensing model for deriving TSM concentration from the Landsat-8 satellite image with a high spatial resolution (30 m). The model validation showed a good performance, with determination coefficient, root-mean-square error, bias, and mean absolute percentage error of 0.72, 6.59 g/m3, 0.72 g/m3 and 29.8%, respectively. Subsequently, the proposed model was applied to generate TSM products in the mussel culture area using Landsat-8 satellite images in different seasons, and the spatial and temporal variations of TSM were further studied.
-
海水养殖业是我国粮食安全保障体系中的重要组成部分[1]，为了解决渔业资源与生态环境问题，“海洋牧场”这一新型的模式近年来快速发展起来。“海洋牧场”是指利用自然海洋生态环境，对鱼、虾、贝、藻等海洋资源进行有计划和有目的的海上放养[2]。海洋牧场既能养护生物资源，又能修复生态环境，是实现我国近海渔业资源恢复、生态系统和谐发展与“蓝色碳汇”的重要途径[3]。海洋牧场的发展依赖于健康的海洋生态系统[4]，因此对牧场生态环境的有效监测是极为重要的工作。
总悬浮颗粒物（total suspended matter, TSM）、叶绿素a、浊度等环境因子对海洋牧场中的生物生长有着重要影响，其中TSM是指悬浮在水中的超过一定大小的物质，包括不溶于水的无机物、有机物（藻类等）以及泥沙、黏土、微生物等。TSM浓度是衡量水体清澈程度和水污染程度的重要指标，是重要的水色和水环境遥感参数[5-7]，影响着海水的透明度和初级生产力，进而影响水生生物的生存和繁殖，因此，TSM的有效监测对海洋牧场环境评估管理具有重要意义。
针对海水TSM浓度的监测，通常采用离散的水样调查法，该方法不但耗时耗力，而且只能获得时空不连续的数据。相比之下卫星遥感技术具有高时空观测优势，能够实时或准实时对海域进行连续观测，及时、客观地掌握海域的TSM实际状况。因此，卫星遥感技术目前已成为监测海洋TSM的重要手段。随着海洋水色遥感技术的不断发展，诸多水色卫星传感器发射成功并用于反演监测TSM浓度，如宽视场海洋观测传感器（sea-viewing wide field-of-view sensor, SeaWiFS）、中分辨率成像光谱仪（moderate-resolution imaging spectroradiometer, MODIS）、中等分辨率成像频谱仪（medium resolution imaging spectrometer, MERIS）、地球静止海洋水色成像仪（geo-stationary ocean color imager, GOCI）等。同时，研究学者们也针对不同传感器、不同海域提出了多种TSM遥感反演算法[8-11]。例如，1994 年 Tassan[8]利用SeaWiFS辐射计490 nm、555 nm和670 nm波段遥感反射率反演了TSM浓度；Zhang等[9]针对黄东海海域，提出了利用MODIS数据的TSM浓度反演算法。He[10]等利用GOCI数据开发了区域TSM浓度算法，并分析了沿海悬浮颗粒物的日内变化。
需要指出的是，现有常用海洋水色传感器空间分辨率多为1 km左右，其TSM遥感产品主要针对大尺度海域。但是，海洋牧场贻贝养殖区的空间尺度通常较小（多为几公里），而且受水动力环境和人为扰动等因素综合影响，海洋牧场水体光学特性复杂多变。这使得现有海洋水色传感器的TSM产品，难以满足对海洋牧场小尺度海域的空间精细化监测需求。因此，有必要针对海洋牧场小尺度区域，开发基于高空间分辨率卫星影像的TSM浓度反演技术，进而构建TSM浓度的高质量遥感产品。事实上，国内外已有研究学者尝试利用Landsat、高分系列等的陆地卫星开展近海区域的TSM研究[12-14]。例如，Zhang等[12]利用Landsat TM / ETM +数据反演了黄河口悬浮颗粒物浓度；Qiu等[13]利用Landsat-8 OLI数据分析了黄河口的总悬浮颗粒物分布变化特征；邵宇杰等[14]针对高分4号卫星（GF-4），构建了杭州湾悬浮泥沙反演模型。这些研究表明利用陆地卫星开展海洋水体TSM浓度遥感反演是可行的。
本文以浙江嵊泗枸杞岛海洋牧场（贻贝养殖区）为研究对象，基于多个航次的现场实测数据，面向高空间分辨率（30 m）的Landsat-8卫星影像，研发TSM浓度遥感反演模型，构建不同季节的TSM卫星遥感产品，并分析其时空分布特征，为海洋牧场环境监测评估提供科学支撑。
1 材料与方法
1.1 研究区域
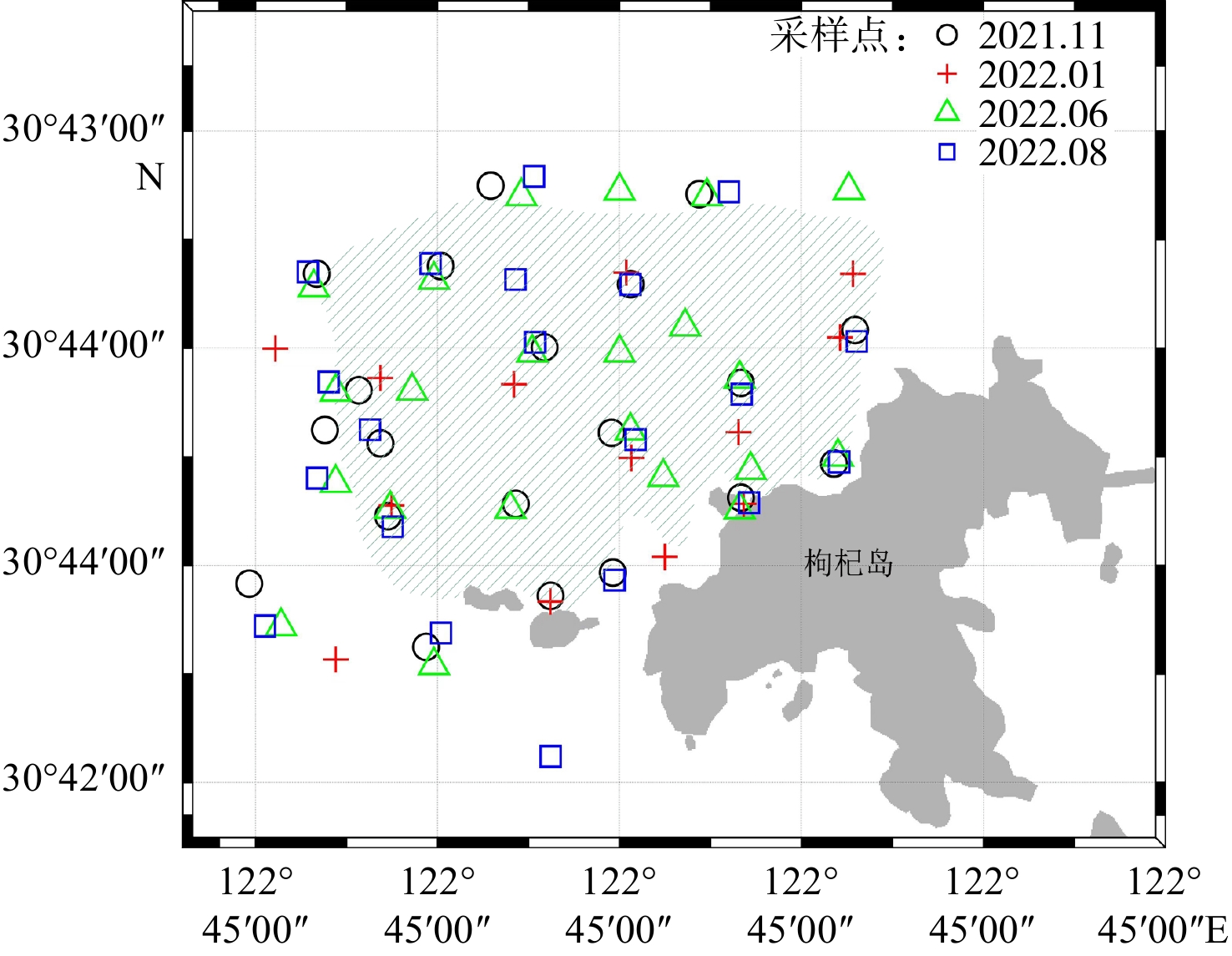
本文研究区域为浙江嵊泗枸杞岛贻贝养殖区及毗邻海域，具体范围为：30.695°N－30.760°N，122.717°E－122.800°E（图1）。枸杞岛是浙江省嵊泗列岛最东边的海岛之一，位于浙江省舟山市东北方向，处于长江与东海交汇的入海口。贻贝养殖区位于枸杞岛西北部近岸海域，面积约1020 hm2，一年可孕育贻贝近10万吨，因此素有“海上牧场”之称，是“中国贻贝”的主产地。
![]()
图 1 研究区域及航次调查站点分布（图中斜线区域为贻贝养殖区）Fig. 1 Study region and sampling locations of each cruise1.2 现场调查数据
本研究分别于2021年11月（秋）和2022年1月（冬）、6月初（晚春）、8月（夏）不同季节在贻贝养殖区及毗邻海域进行了4个航次调查实验。每个现场航次调查在贻贝养殖区及毗邻海域布设20个站点，站点位置如图1所示。调查参数包括水体的遥感反射率（Rrs）和TSM浓度等。参数调查及测量过程严格按照NASA海洋光学规范进行[15]。
TSM浓度采用称重法测量获取[16]，主要步骤包括烘干、冷却、称重、过滤、再烘干、再冷却、再称重。具体过程：在航次开展之前，先在实验室内利用烘箱在110 ℃条件下对空白GF/F滤膜进行烘干，待在干燥皿中冷却后，利用十万分之一精度的天平进行称重，计为w1；在开展航次调查时，利用事先称重过的空白滤膜过滤0.5～1 L的水样，过滤后将滤膜保存在−20 ℃冰箱中，待调查结束后，将滤膜带回实验室进行再次烘干、冷却及称重，此时重量计为w2。TSM浓度使用以下公式计算：
$$ {C_{{\text{TSM}}}}{\text{ = }}\frac{{{w_1} - {w_2}}}{V} $$ (1) 式中：CTSM表示TSM的浓度（g/m3）；V为过滤水样体积（m3）。
遥感反射率Rrs利用ASD便携式野外光谱仪FieldSpec® Pro FR（波长范围：350～2500 nm）现场测得，测量方法为水面以上测量法[15,17-18]。主要流程如下：在天空晴朗无云时，根据调查船停靠方位和太阳光情况，确定测量方位角和天顶角分别为135°和40°[17]；然后，利用ASD便携式野外光谱仪测量参考灰板、水体和天空光的辐亮度光谱，对于每个目标物分别测量10次光谱，然后去除异常光谱后计算剩余光谱平均值；最后，计算得到遥感反射率Rrs(λ)：
$$ {R_{{\text{rs}}}}(\lambda ) = \frac{{{L_{\text{t}}}(\lambda ) - \rho {L_{{\text{sky}}}}(\lambda )}}{{\pi {L_{\text{p}}}(\lambda )/{\rho _{\text{p}}}}} $$ (2) 式中：Lt(λ)、Lsky(λ)和Lp(λ)分别为水体、天空光和参考灰板的辐亮度；ρp为参考灰板的漫反射率，由参考灰板生产商提供；ρ为水—气界面对天空光的反射率，与风速、风向、观测几何角度以及太阳位置有关，当水面平静时，ρ一般取值0.022[18]。将Rrs(λ)数据与现场实测TSM浓度数据进行匹配，共得到76组样本。
为了构建面向Landsat-8卫星影像的TSM浓度遥感反演模型，本研究利用美国地质勘探局（United States Geological Survey，USGS）官网（https://earthexplorer.usgs.gov/）给出的Landsat-8 OLI传感器光谱响应函数，将所有站点的实测Rrs(λ)重采样到Landsat-8 OLI波段，计算公式[9]为：
$$ {R_{{\text{rs}}}}\left( {{\lambda _k}} \right) = \frac{{\displaystyle\int_{{\lambda _i}}^{{\lambda _j}} {S\left( \lambda \right){R_{{\text{rs}}}}\left( \lambda \right)d\lambda } }}{{\displaystyle\int_{{\lambda _i}}^{{\lambda _j}} {S\left( \lambda \right)d\lambda } }} $$ (3) 式中：λk为Landsat-8 OLI波段的中心波长；λi和λj分别为中心波长λk的下限和上限；S(λ)为光谱响应函数；Rrs(λ)为所有站点现场实测的遥感反射率。
1.3 卫星遥感数据
本研究使用的卫星数据来自Landsat-8卫星的L1级产品。Landsat-8携带有OLI和TIRS传感器，OLI成像仪包括9个波段，时间分辨率为16 d，空间分辨率为30 m，其中包括一个空间分辨率15 m的全色波段。本文选取前5个波段（中心波长为：443 nm、482 nm、561 nm、655 nm和865 nm）进行TSM浓度的反演。针对研究区域，本文从USGS官网（https://earthexplorer.usgs.gov/）下载获得了2021年11月16日（秋季）、2022年1月3日（冬季）、2022年3月24日（春季）和2022年8月15日（夏季）4景晴空无云的影像，并将遥感图像裁切至本文所需的研究区域，真彩色合成影像如图2所示。
大气校正是海洋水色遥感反演海洋光学和生物参数的关键过程[19]。本文利用ACOLITE (Atmospheric Correction for OLI lite) 20220222.0版本（下载网址：http://odnature.naturalsciences.be/remsem/software-and-data/acolite/）对Landsat-8 OLI卫星影像数据进行大气校正。ACOLITE是一种专门针对高浊度近岸水体的大气校正方法，被广泛用于近岸及内陆湖泊水色遥感研究领域[20-22]。ACOLITE包含默认的“暗光谱拟合”（dark spectrum fitting, DSF）和“指数外推”（exponential extrapolation, EXP）两种大气校正算法。DSF算法是针对米级分辨率传感器开发的，对于高分辨率卫星传感器其算法性能优于EXP算法，基于现场实测数据的验证表明，在大多数情况下DSF算法的误差小于EXP算法，其均方根误差小于0.01，而EXP算法的误差较大，均方根误差有时超过0.02[22]。因此，本研究采用了DSF算法进行大气校正。
1.4 模型精度评价指标
本文利用留一交叉检验法对模型精度进行验证，精度评价指标包括：决定系数（determination coefficient, R2）、平均偏差（Bias）、均方根误差（root-mean-square error, RMSE）及平均绝对百分误差（mean absolute percentage error, MAPE），计算公式分别为：
$$ {R^2} = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^N {{{\left( {{{\hat y}_i} - {y_i}} \right)}^2}} }}{{\displaystyle\sum\limits_{i = 1}^N {{{\left( {\bar y - {y_i}} \right)}^2}} }} = \frac{{\displaystyle\sum\limits_{i = 1}^N {{{\left( {{{\hat y}_i} - \bar y} \right)}^2}} }}{{\displaystyle\sum\limits_{i = 1}^N {{{\left( {{y_i} - \bar y} \right)}^2}} }} $$ (4) $$ Bias = \frac{1}{N}\sum\limits_{i = 1}^N {({y_i} - {{\hat y}_i})} $$ (5) $$ MAPE{\text{ }} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {\frac{{{y_{\text{i}}} - {{\hat y}_i}}}{{{y_i}}}} \right|} \times 100\% $$ (6) $$ RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{y_{\text{i}}} - {{\hat y}_i}} \right)}^2}} } $$ (7) 式中：
$ {y_i} $ （i=1,2,···,N）表示现场实测TSM浓度；$ \bar y $ 为现场实测TSM浓度平均值；$ {\hat y_i} $ 表示TSM浓度反演值；N为样本数量。2 结果与讨论
2.1 现场实测悬浮颗粒物浓度及遥感反射率光谱分布特征
不同季节4个航次调查实测的TSM浓度数据呈现出明显的变化特征（表1），可以看出：贻贝养殖区及毗邻海域所有季节的实测TSM浓度范围为 2.2 ～ 45.4 g/m3，其平均值、方差和变异系数分别为10.9 g/m3、11.0 g/m3和100.9%；4个季度的TSM浓度分布也呈现出明显的差异，整体上冬季TSM浓度最高，均值（Mean）高达27.7 g/m3，变异系数（coefficient of variation，CV）也最大（124.4%），而秋季、晚春和夏季3个季节的TSM浓度值则相当。在冬季现场航次调查前3 d，研究区域遭遇强风天气，这可能引起了海水上下强烈混合，导致底层悬浮颗粒物再悬浮，进而使得表层海水TSM浓度升高。这些结果表明研究区域的TSM浓度具有显著的变异性。
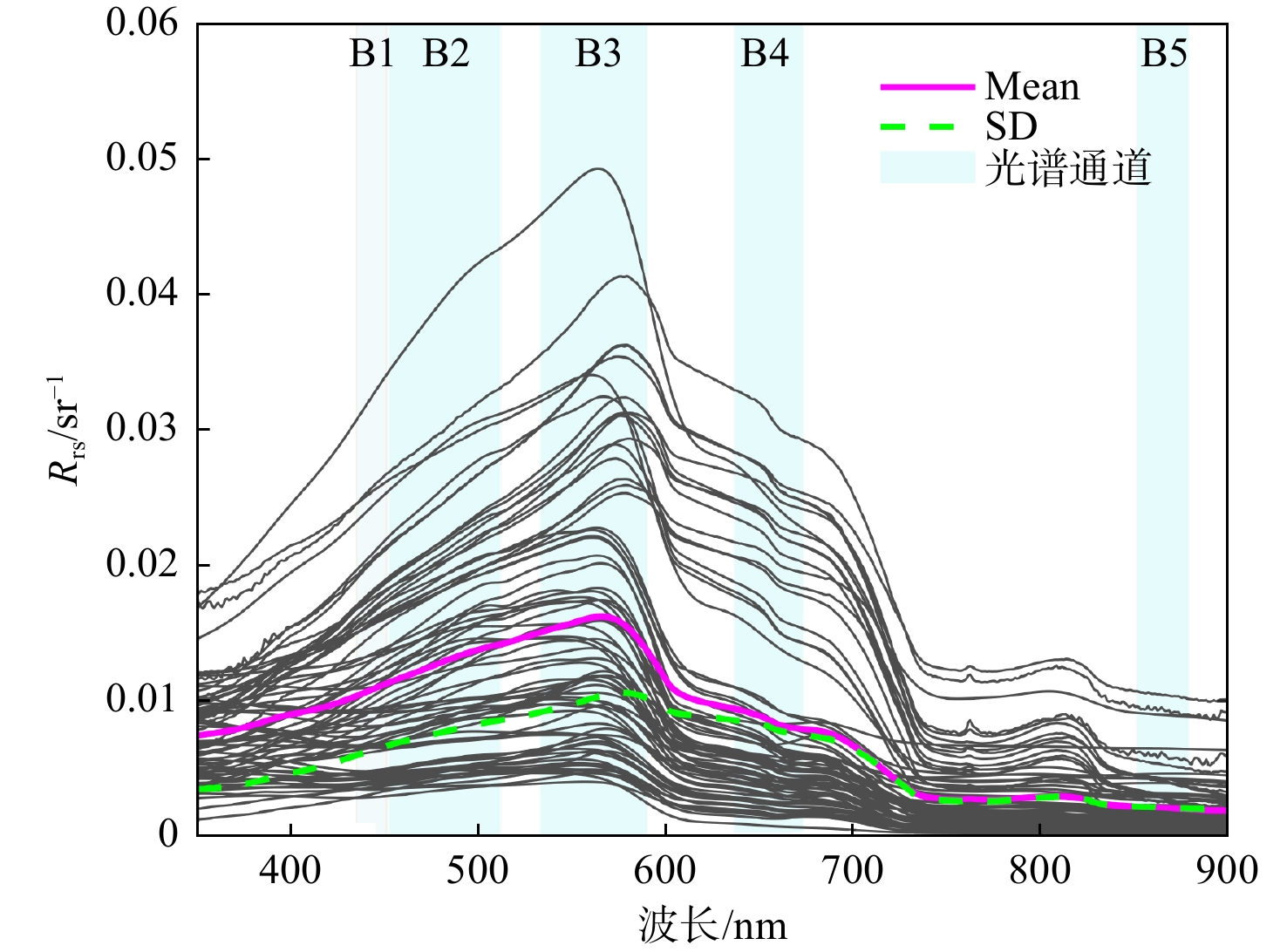
表 1 实测总悬浮颗粒物浓度的分布特征Tab. 1 Variations of measured total suspended matter concentration时间 最大值 / g·m−3 最小值/ g·m−3 平均值/ g·m−3 标准差/ g·m−3 变异系数 / (%) 2021-11 18.7 2.2 6.3 3.8 60.5 2022-01 43.0 13.7 27.7 8.6 31.2 2022-06 45.4 3.0 7.5 9.4 124.4 2022-08 8.3 3.3 5.0 1.5 29.2 总量 45.4 2.2 10.9 11.0 100.9 相应地，受TSM浓度的高度变化影响，遥感反射率Rrs(λ)光谱也呈现出了明显的变化（图3）。由图3可以看出： Rrs(λ)光谱值在蓝绿波段随波长的增加而增大，在550～580 nm波长范围达到峰值，这主要是由于该波长处TSM有着较高的后向散射[23]。此外，部分样本的Rrs(λ)光谱在600～700 nm波长范围有着明显的“肩状”特征，同时在810 nm波长附近出现第二反射峰，这些特征均为典型的浑浊水体Rrs(λ)光谱特征[23]。
![]()
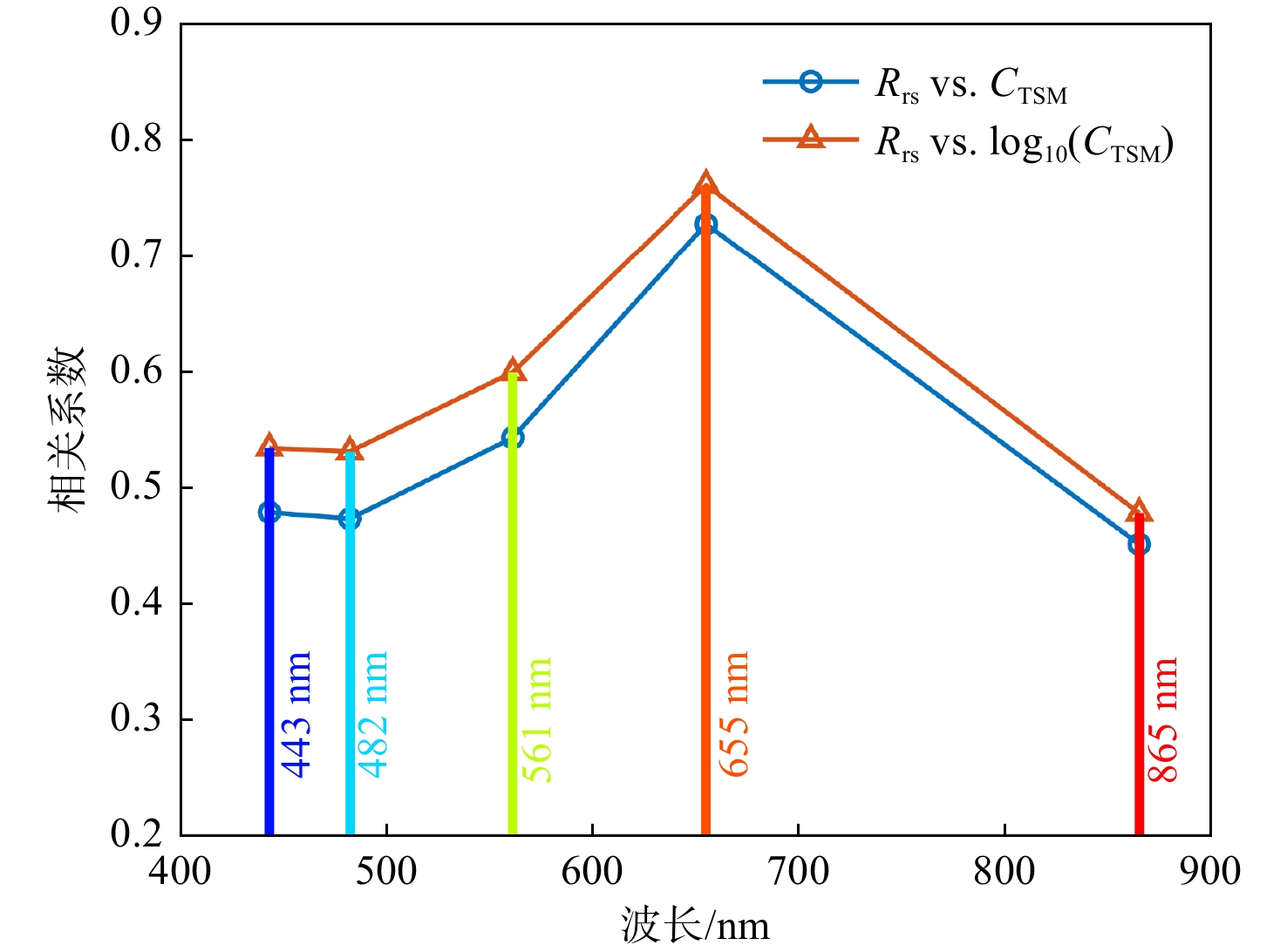
图 3 现场实测Rrs(λ)光谱曲线图中蓝色柱子表示Landsat8 OLI传感器的前5个光谱通道Fig. 3 In situ measured Rrs(λ) spectra进一步，为了探究Rrs(λ)光谱对TSM浓度变化的响应特征，本文分析了TSM浓度与光谱之间的关系。图4展示了Landsat-8 OLI各个波段Rrs(λ)与TSM浓度（CTSM）以及对数转换后的TSM浓度[log10(CTSM)]之间的相关性，可以看出：Rrs(λ)与CTSM以及log10(CTSM)均呈现显著相关性，相关系数均大于0.5；同时，Rrs(λ)与log10(CTSM)之间的相关性均强于与CTSM的相关性；Rrs(λ)与log10(CTSM)之间的相关系数最大值为0.77（最大值出现在650 nm附近）。以上显著相关性结果表明Rrs(λ)具有很大的潜力用于TSM浓度反演，而且在建立TSM反演模型时，相比 CTSM，log10(CTSM)作为模型因变量可能会有更好的建模精度。
![]()
图 4 Rrs(λ)与TSM浓度（CTSM）以及对数转换后的TSM浓度[log10(CTSM)]之间的相关性Fig. 4 Correlation coefficient of Rrs(λ) with CTSM and log10(CTSM)2.2 TSM浓度遥感反演模型构建
为了建立最优的TSM浓度遥感反演模型，本文尝试构建了不同光谱指数形式以充分利用Rrs(λ)信息。如表2所示，本文共建立了8个不同的Rrs(λ)光谱指数。针对每种光谱指数，考虑了所有可能的Landsat-8 OLI波段组合，并分析了不同波段组合下的光谱指数和log10(CTSM)的相关性，在表2中展示了最佳的（即相关系数最大的）波段组合及其相关系数。可以发现：最优波段组合下的每种光谱指数与log10(CTSM)相关系数均大于0.7，其中X4、X5和X8与log10(CTSM)的相关系数最高，均大于0.8。因此，本研究选取X4、X5和X8这3个光谱指数进行后续的TSM浓度反演模型构建。
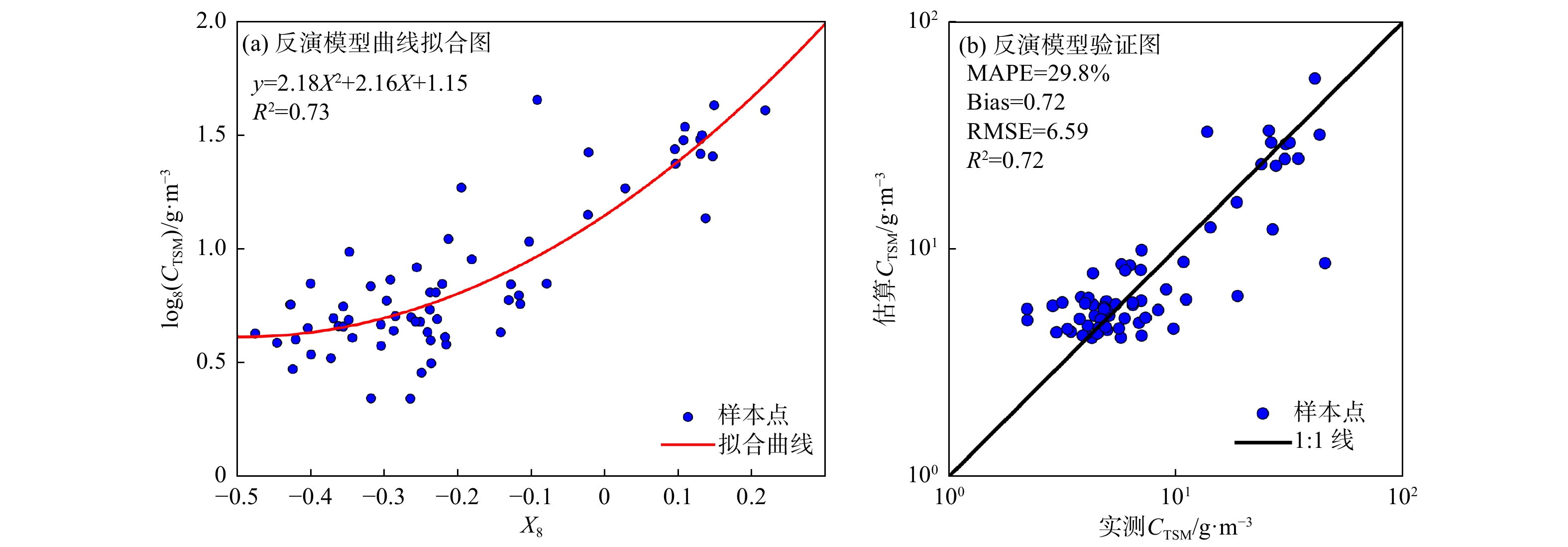
表 2 用于估算TSM浓度的 8 个光谱指数及其与悬浮颗粒物浓度的相关性Tab. 2 Eight spectral indexes for deriving TSM concentrations and their correlations with TSM concentrationsX 光谱指数 最佳波段组合 相关系数 X1 ${R_{{\text{rs}}}}\left( {{\lambda _1}} \right)$ ${\lambda _1}$ = 655 nm 0.76 X2 $\lg \left[ {{R_{{\text{rs}}}}\left( {{\lambda _1}} \right)} \right]$ ${\lambda _1}$ = 655 nm 0.71 X3 ${R_{{\text{rs}}}}\left( {{\lambda _1}} \right) - {R_{{\text{rs}}}}\left( {{\lambda _{\text{2}}}} \right)$ ${\lambda _1}$ = 865 nm and ${\lambda _2}$=655 nm 0.77 X4 $\dfrac{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right)}}{{{R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}$ ${\lambda _1}$ = 655 nm and ${\lambda _2}$=443 nm 0.85 X5 $\lg \left[ {\dfrac{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right)}}{{{R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}} \right]$ ${\lambda _1}$ = 655 nm and ${\lambda _2}$=443 nm 0.82 X6 $\dfrac{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right) - {R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right)/{R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}$ ${\lambda _1}$ = 561 nm and ${\lambda _2}$=482 nm 0.71 X7 $\dfrac{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right) + {R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right)/{R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}$ ${\lambda _1}$ = 443 nm and ${\lambda _2}$=655 nm 0.79 X8 $\dfrac{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right) - {R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right) + {R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}$ ${\lambda _1}$ = 655 nm and ${\lambda _2}$=443 nm 0.83 进一步，针对光谱指数X4、X5和X8，分别建立与 log10(CTSM)的线性模型、指数模型、二次模型以及幂函数模型，并计算各反演模型的R2、MAPE、RMSE和Bias，结果列于表3。从表3可以看出：光谱指数X4对应的线性模型和幂函数模型、光谱指数X4对应的指数模型和二次函数模型、X8对应的指数模型和二次函数模型均表现出良好的反演效果。相比之下，X8对应的二次函数模型反演效果最优，同时具有较高的R2（0.73）以及较低的RMSE（6.28 g/m3）、Bias（0.71 g/m3）和MAPE（29.0%），其模型拟合效果如图5a所示，多数样本点能够较好地分布在拟合曲线附近。因此，该模型被最终确定为 TSM 浓度的最优反演模型，其表达式如下：
表 3 悬浮颗粒物浓度反演模型对比Tab. 3 Comparisons of the performance of different estimation models of total suspended matter concentration光谱指数 模型形式 模型方程 R2 MAPE/（%） Bias/
g·m−3RMSE/
g·m−3${X_4}{\text{ = }}\dfrac{{{R_{{\text{rs}}}}\left( {{\text{655}}} \right)}}{{{R_{{\text{rs}}}}\left( {{\text{443}}} \right)}}$ 幂函数模型 y = 1.17x0.81 0.71 34.5 0.94 6.25 指数模型 y = 0.43exp(0.92x) 0.45 33.9 0.58 8.13 线性模型 y = 0.99x+0.20 0.72 34.0 0.91 6.33 二次模型 y = 704.51x2−24.16x+0.65 0.63 39.6 1.23 8.24 ${X_5}{\text{ = }}\lg \left[ {\dfrac{{{R_{{\text{rs}}}}\left( {{\text{655}}} \right)}}{{{R_{{\text{rs}}}}\left( {{\text{443}}} \right)}}} \right]$ 幂函数模型 y = 0.54x−0.28 0.61 53.9 1.85 11.71 指数模型 y = 1.17exp(1.87x) 0.71 34.5 0.94 6.25 线性模型 y = 1.72x+1.19 0.45 39.0 1.41 6.44 二次模型 y = 2.91x2−2.47x+1.15 0.73 32.3 0.71 6.62 ${X_8}{\text{ = }}\dfrac{{{R_{{\text{rs}}}}\left( {{\text{655}}} \right) - {R_{{\text{rs}}}}\left( {{\text{443}}} \right)}}{{{R_{{\text{rs}}}}\left( {{\text{655}}} \right) + {R_{{\text{rs}}}}\left( {{\text{443}}} \right)}}$ 幂函数模型 y = 0.56x−0.28 0.62 54.1 1.85 11.76 指数模型 y = 1.16(1.68x) 0.73 33.9 0.90 6.26 线性模型 y = 1.58x+1.19 0.49 37.7 1.32 6.33 二次模型 y = 2.18x2−2.16x+1.15 0.73 29.0 0.71 6.28 ![]()
图 5 TSM浓度反演模型拟合与验证Fig. 5 Model fitting and validation for estimation of TSM concentration$$ {C_{{\text{TSM}}}} = {\text{ }}{10^{2.1{\text{8}}{X^2}{\text{ }} + {\text{ }}2.16X + {\text{ }}1.1{\text{5}}}} $$ (8) $$ X{\text{ = }}\frac{{{R_{{\text{rs}}}}\left( {{\text{655}}} \right) - {R_{{\text{rs}}}}\left( {{\text{443}}} \right)}}{{{R_{{\text{rs}}}}\left( {{\text{655}}} \right) + {R_{{\text{rs}}}}\left( {{\text{443}}} \right)}} $$ (9) 为了进一步验证所建立的 TSM 浓度反演模型的精度，对其进行了留一法交叉检验，结果如图5b所示：整体上TSM浓度的反演值和实测值具有较好的一致性，绝大多数样本均匀分布在1∶1线附近，交叉检验的R2、RMSE、Bias和MAPE分别为0.72、6.59 g/m3、0.72 g/m3和29.8%。这些结果表明本研究针对贻贝养殖区小尺度区域所建立的TSM浓度反演模型具有良好的估算精度。
需要指出的是，本研究区的贻贝养殖方式主要为浮筏吊养，虽然网箱等布放在水面以下，但漂浮在水面以上的浮标（分布稀疏）可能会对水体遥感反射率产生一定的影响。为此，分别统计分析了养殖区内、外大量的遥感反射率光谱，发现浮标潜在的影响主要存在于近红外和短波红外波段，而在可见光波段的影响较小，这使得本文所构建的TSM反演模型受其影响也较小。而要想获得更精确的TSM遥感产品，需考虑贻贝养殖区内浮标的潜在影响，并对其进行相应的校正。此外，本文开发的反演模型主要针对枸杞岛贻贝养殖区及毗邻海域，模型在其他海洋牧场区的适用性还有待进一步检验。本文利用了Landsat-8 OLI影像对贻贝养殖区TSM浓度进行了反演，对于其他高分辨率卫星传感器（如Sentinel-2、环境卫星等），也需要根据其传感器波段设置，进一步研究开发相应的TSM浓度遥感反演模型，以实现利用多源卫星传感器数据的海洋牧场水环境要素监测，这些问题将在下一步工作中深入研究。
2.3 基于Landsat-8影像的TSM浓度反演
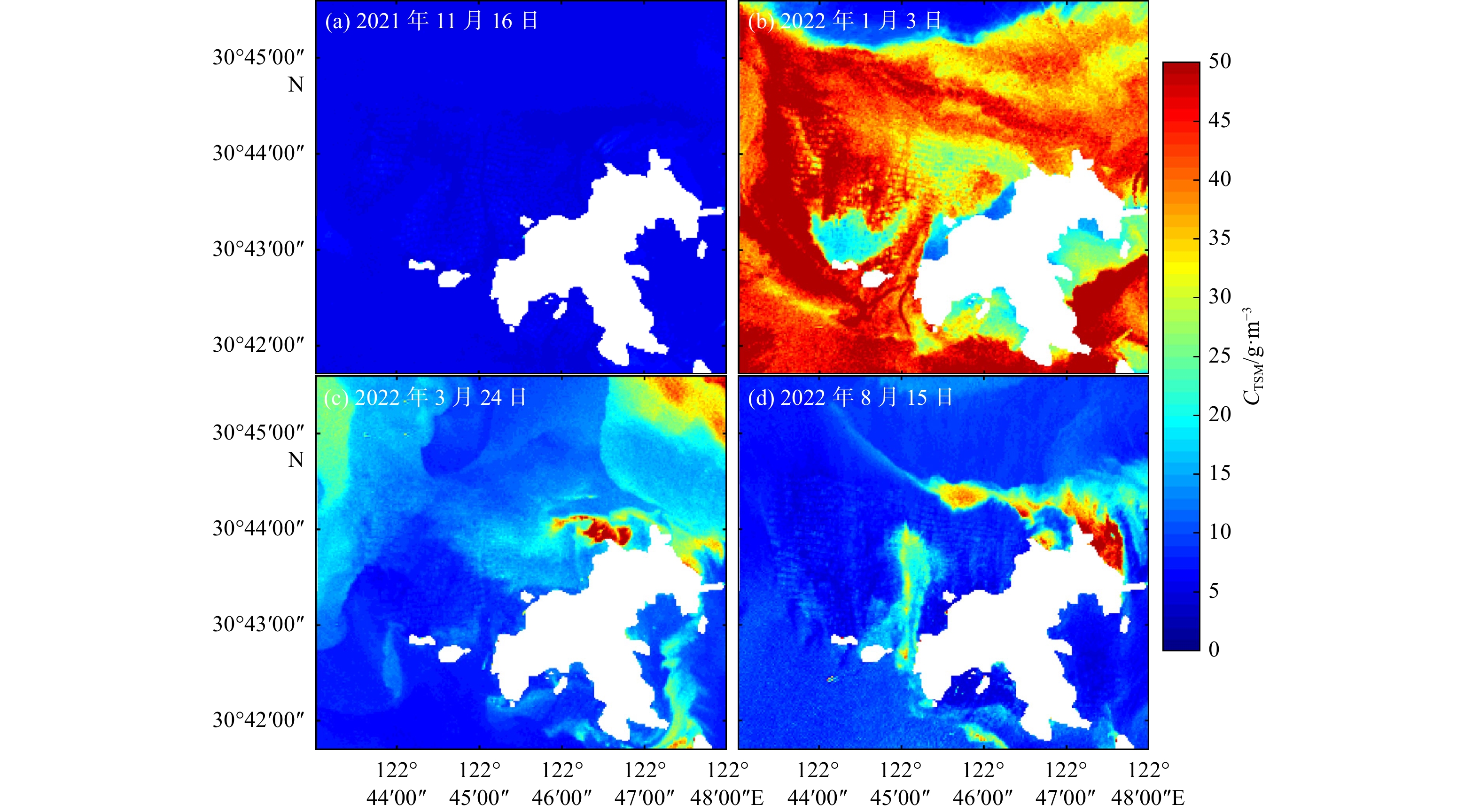
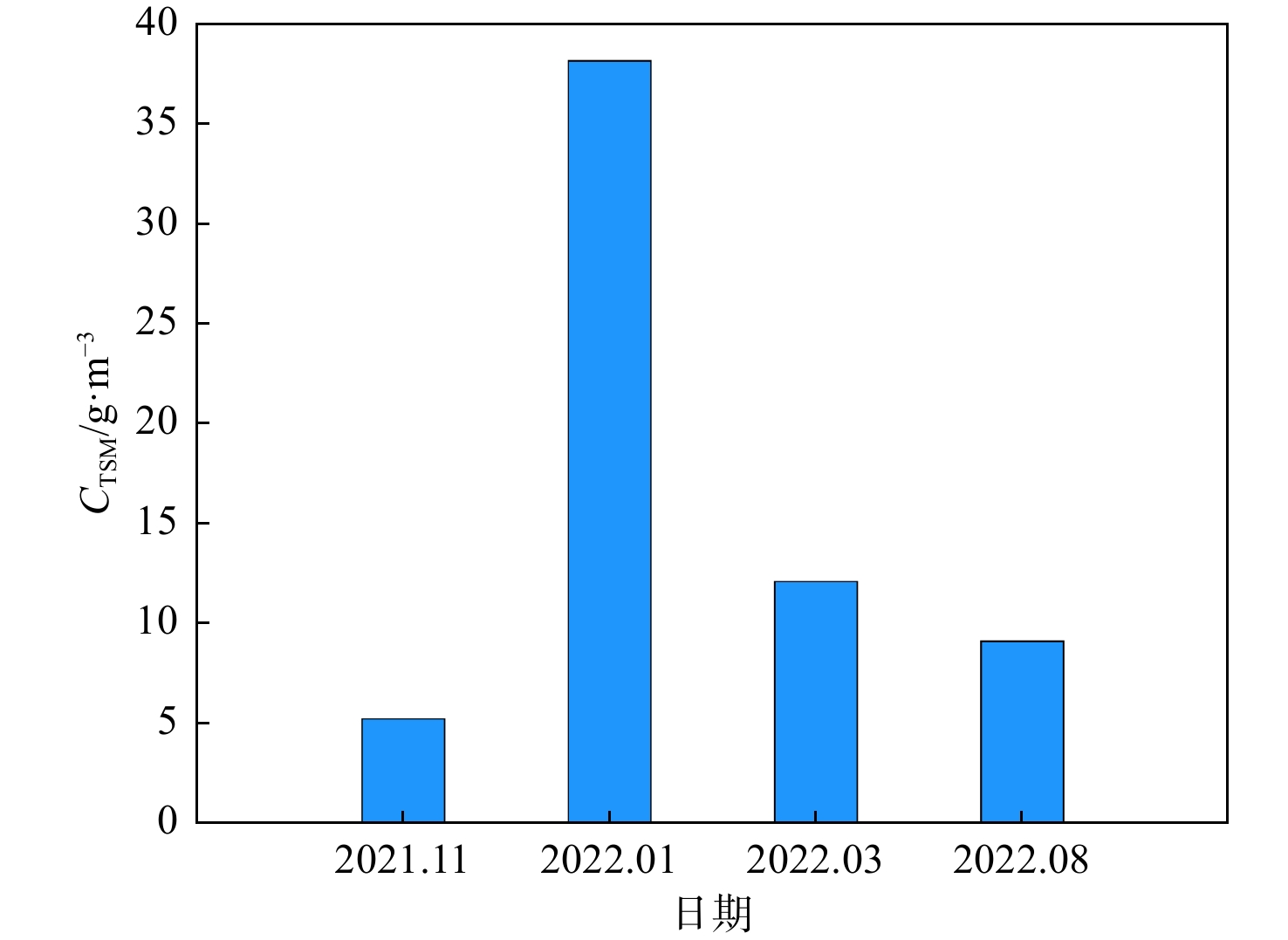
将本文开发的TSM浓度遥感反演模型应用于2021年11月16日（秋季）、2022年1月3日（冬季）、2022年3月24日（春季）和2022年8月15日（夏季）大气校正后的Landsat-8 OLI卫星影像，反演得到了4个季节的TSM浓度遥感产品（图6），同时，也根据图1所示的贻贝养殖区范围，统计分析了养殖区的TSM浓度平均值（图7）。可以看出：2021年秋季（2021年11月）（图6a），贻贝养殖区及毗邻海域的TSM浓度较低，贻贝养殖区的TSM浓度平均值为5.3 g/m3；冬季（2022年1月）（图6b），贻贝养殖区及毗邻海域的TSM浓度最高，大多数区域的TSM浓度大于45 g/m3；春季（2022年3月）（图6c），贻贝养殖区及毗邻海域大部分海域的TSM浓度有所升高，海域牧场大部分区域TSM浓度在12 g/m3左右，这可能和春季常发生的浮游植物藻华有关，浮游植物藻华增加了有机悬浮颗粒物，进而使得TSM浓度升高；夏季（2022年8月）（图6d），除少部分区域TSM浓度出现高值外，贻贝养殖区及毗邻海域绝大部分区域TSM浓度较低，浓度为5 ～ 10 g/m3，平均值为9.1 g/m3。正如2.1节所述，2022年1月初（航次调查前3 d），贻贝养殖区经历了一次强风天气，强风触发的海水上下混合可能引起了底层悬浮颗粒物再悬浮，进而导致TSM浓度升高。
![]()
图 6 利用Landsat-8 OLI 影像反演的贻贝养殖区及毗邻海域TSM浓度分布Fig. 6 Distributions of TSM concentrations in the mussel culture area and adjacent areas derived from Landsat-8 OLI satellite images![]()
图 7 贻贝养殖区TSM浓度平均反演值的季节变化Fig. 7 Seasonal variation of the average values of Landsat-8 OLI derived TSM concentrations in the mussel culture area此外，值得注意的是，在冬季贻贝养殖区内部部分区域的TSM浓度明显低于毗邻海域浓度（大于45 g/m3），TSM浓度为20～30 g/m3，这可能和贻贝养殖有关。贻贝养殖采用的养殖方式为浮筏吊养方式，由于浮筏的存在，将养殖区分隔成一个个小区域，在一定程度上减弱了水体的上下混合，抑制了底层悬浮颗粒物再悬浮。同时，仔细观察也可发现，2021年秋季和2022年夏季，贻贝养殖区内部区域的TSM浓度也略低于毗邻海域浓度值，这也可能和养殖区的贻贝摄食方式有关，贻贝属于滤食性贝类，主要以小型的浮游生物、有机碎屑以及一些微生物为食，这可能在一定程度上降低了TSM的浓度[24-26]。
3 结 论
（1）针对海洋牧场（贻贝养殖区）小尺度区域，基于多个海洋牧场航次调查数据，本文建立了面向Landsat-8 OLI影像的TSM浓度遥感反演模型，模型表现出良好的估算精度（R2 = 0.72，RMSE = 6.59 g/m3，Bias = 0.72 g/m3，MAPE = 29.8%）；进而利用该模型得到了贻贝养殖区小尺度区域的TSM浓度空间和季节分布特征。
（2）贻贝养殖区TSM浓度在2021年秋季和2022年夏季最低，在2022年春季有所升高，在2021年冬季达到最高；冬季TSM浓度高可能与海水上下混合引起的底层悬浮颗粒物再悬浮有关。贻贝养殖区内部部分区域TSM浓度明显低于毗邻海域，这可能与贻贝养殖筏架抑制水体上下混合有关。
（3）本研究构建的TSM浓度遥感反演模型为枸杞岛贻贝养殖牧场区TSM浓度快速监测提供了科学支持，进而可服务于贻贝养殖区养殖环境的评估和管理。
-
![]()
图 1 研究区域及航次调查站点分布
（图中斜线区域为贻贝养殖区）
Fig. 1. Study region and sampling locations of each cruise
![]()
图 3 现场实测Rrs(λ)光谱曲线
图中蓝色柱子表示Landsat8 OLI传感器的前5个光谱通道
Fig. 3. In situ measured Rrs(λ) spectra
![]()
图 4 Rrs(λ)与TSM浓度（CTSM）以及对数转换后的TSM浓度[log10(CTSM)]之间的相关性
Fig. 4. Correlation coefficient of Rrs(λ) with CTSM and log10(CTSM)
![]()
图 5 TSM浓度反演模型拟合与验证
Fig. 5. Model fitting and validation for estimation of TSM concentration
![]()
图 6 利用Landsat-8 OLI 影像反演的贻贝养殖区及毗邻海域TSM浓度分布
Fig. 6. Distributions of TSM concentrations in the mussel culture area and adjacent areas derived from Landsat-8 OLI satellite images
![]()
图 7 贻贝养殖区TSM浓度平均反演值的季节变化
Fig. 7. Seasonal variation of the average values of Landsat-8 OLI derived TSM concentrations in the mussel culture area
表 1 实测总悬浮颗粒物浓度的分布特征
Tab. 1 Variations of measured total suspended matter concentration
时间 最大值 / g·m−3 最小值/ g·m−3 平均值/ g·m−3 标准差/ g·m−3 变异系数 / (%) 2021-11 18.7 2.2 6.3 3.8 60.5 2022-01 43.0 13.7 27.7 8.6 31.2 2022-06 45.4 3.0 7.5 9.4 124.4 2022-08 8.3 3.3 5.0 1.5 29.2 总量 45.4 2.2 10.9 11.0 100.9 
下载: 导出CSV
表 2 用于估算TSM浓度的 8 个光谱指数及其与悬浮颗粒物浓度的相关性
Tab. 2 Eight spectral indexes for deriving TSM concentrations and their correlations with TSM concentrations
X 光谱指数 最佳波段组合 相关系数 X1 ${R_{{\text{rs}}}}\left( {{\lambda _1}} \right)$ ${\lambda _1}$ = 655 nm 0.76 X2 $\lg \left[ {{R_{{\text{rs}}}}\left( {{\lambda _1}} \right)} \right]$ ${\lambda _1}$ = 655 nm 0.71 X3 ${R_{{\text{rs}}}}\left( {{\lambda _1}} \right) - {R_{{\text{rs}}}}\left( {{\lambda _{\text{2}}}} \right)$ ${\lambda _1}$ = 865 nm and ${\lambda _2}$=655 nm 0.77 X4 $\dfrac{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right)}}{{{R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}$ ${\lambda _1}$ = 655 nm and ${\lambda _2}$=443 nm 0.85 X5 $\lg \left[ {\dfrac{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right)}}{{{R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}} \right]$ ${\lambda _1}$ = 655 nm and ${\lambda _2}$=443 nm 0.82 X6 $\dfrac{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right) - {R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right)/{R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}$ ${\lambda _1}$ = 561 nm and ${\lambda _2}$=482 nm 0.71 X7 $\dfrac{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right) + {R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right)/{R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}$ ${\lambda _1}$ = 443 nm and ${\lambda _2}$=655 nm 0.79 X8 $\dfrac{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right) - {R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}{{{R_{{\text{rs}}}}\left( {{\lambda _1}} \right) + {R_{{\text{rs}}}}\left( {{\lambda _2}} \right)}}$ ${\lambda _1}$ = 655 nm and ${\lambda _2}$=443 nm 0.83
下载: 导出CSV
表 3 悬浮颗粒物浓度反演模型对比
Tab. 3 Comparisons of the performance of different estimation models of total suspended matter concentration
光谱指数 模型形式 模型方程 R2 MAPE/（%） Bias/
g·m−3RMSE/
g·m−3${X_4}{\text{ = }}\dfrac{{{R_{{\text{rs}}}}\left( {{\text{655}}} \right)}}{{{R_{{\text{rs}}}}\left( {{\text{443}}} \right)}}$ 幂函数模型 y = 1.17x0.81 0.71 34.5 0.94 6.25 指数模型 y = 0.43exp(0.92x) 0.45 33.9 0.58 8.13 线性模型 y = 0.99x+0.20 0.72 34.0 0.91 6.33 二次模型 y = 704.51x2−24.16x+0.65 0.63 39.6 1.23 8.24 ${X_5}{\text{ = }}\lg \left[ {\dfrac{{{R_{{\text{rs}}}}\left( {{\text{655}}} \right)}}{{{R_{{\text{rs}}}}\left( {{\text{443}}} \right)}}} \right]$ 幂函数模型 y = 0.54x−0.28 0.61 53.9 1.85 11.71 指数模型 y = 1.17exp(1.87x) 0.71 34.5 0.94 6.25 线性模型 y = 1.72x+1.19 0.45 39.0 1.41 6.44 二次模型 y = 2.91x2−2.47x+1.15 0.73 32.3 0.71 6.62 ${X_8}{\text{ = }}\dfrac{{{R_{{\text{rs}}}}\left( {{\text{655}}} \right) - {R_{{\text{rs}}}}\left( {{\text{443}}} \right)}}{{{R_{{\text{rs}}}}\left( {{\text{655}}} \right) + {R_{{\text{rs}}}}\left( {{\text{443}}} \right)}}$ 幂函数模型 y = 0.56x−0.28 0.62 54.1 1.85 11.76 指数模型 y = 1.16(1.68x) 0.73 33.9 0.90 6.26 线性模型 y = 1.58x+1.19 0.49 37.7 1.32 6.33 二次模型 y = 2.18x2−2.16x+1.15 0.73 29.0 0.71 6.28
下载: 导出CSV
-
[1] 陈 勇, 田 涛, 刘永虎, 等. 我国海洋牧场发展现状、问题及对策(上)[J]. 科学养鱼, 2022 (2): 24-25. doi: 10.3969/j.issn.1004-843X.2022.02.012 [2] 陈力群, 张朝晖, 王宗灵. 海洋渔业资源可持续利用的一种模式——海洋牧场[J]. 海岸工程, 2006, 25(4): 71-76. doi: 10.3969/j.issn.1002-3682.2006.04.011 [3] 林承刚, 杨红生, 陈 鹰, 等. 现代化海洋牧场建设与发展——第230期双清论坛学术综述[J]. 中国科学基金, 2021, 35(1): 143-152. doi: 10.16262/j.cnki.1000-8217.20200825.005 [4] 杨红生. 我国海洋牧场建设回顾与展望[J]. 水产学报, 2016, 40(7): 1133-1140. [5] DOXARAN D, CASTAING P, LAVENDER S J. Monitoring the maximum turbidity zone and detecting fine-scale turbidity features in the Gironde estuary using high spatial resolution satellite sensor (SPOT HRV, Landsat ETM+) data[J]. International Journal of Remote Sensing, 2006, 27(11): 2303-2321. doi: 10.1080/01431160500396865
[6] SHEN F, VERHOEF W, ZHOU Y X, et al. Satellite estimates of wide-range suspended sediment concentrations in Changjiang (Yangtze) estuary using MERIS data[J]. Estuaries and Coasts, 2010, 33(6): 1420-1429. doi: 10.1007/s12237-010-9313-2
[7] ODERMATT D, GITELSON A, BRANDO V E, et al. Review of constituent retrieval in optically deep and complex waters from satellite imagery[J]. Remote Sensing of Environment, 2012, 118: 116-126. doi: 10.1016/j.rse.2011.11.013
[8] TASSAN S. Local algorithms using SeaWiFS data for the retrieval of phytoplankton, pigments, suspended sediment, and yellow substance in coastal waters[J]. Applied Optics, 1994, 33(12): 2369-2378. doi: 10.1364/AO.33.002369
[9] ZHANG M W, TANG J W, DONG Q, et al. Retrieval of total suspended matter concentration in the Yellow and East China Seas from MODIS imagery[J]. Remote Sensing of Environment, 2010, 114(2): 392-403. doi: 10.1016/j.rse.2009.09.016
[10] HE X Q, BAI Y, PAN D L, et al. Using geostationary satellite ocean color data to map the diurnal dynamics of suspended particulate matter in coastal waters[J]. Remote Sensing of Environment, 2013, 133: 225-239. doi: 10.1016/j.rse.2013.01.023
[11] SISWANTO E, TANG J W, YAMAGUCHI H, et al. Empirical ocean-color algorithms to retrieve chlorophyll-a, total suspended matter, and colored dissolved organic matter absorption coefficient in the Yellow and East China Seas[J]. Journal of Oceanography, 2011, 67(5): 627-650. doi: 10.1007/s10872-011-0062-z
[12] ZHANG M W, DONG Q, CUI T W, et al. Suspended sediment monitoring and assessment for Yellow River estuary from Landsat TM and ETM+ imagery[J]. Remote Sensing of Environment, 2014, 146: 136-147. doi: 10.1016/j.rse.2013.09.033
[13] QIU Z F, XIAO C, PERRIE W, et al. Using Landsat 8 data to estimate suspended particulate matter in the Yellow River estuary[J]. Journal of Geophysical Research:Oceans, 2017, 122(1): 276-290. doi: 10.1002/2016JC012412
[14] 邵宇杰, 胡越凯, 周 斌, 等. 基于GF-4卫星的杭州湾悬浮泥沙浓度遥感监测研究[J]. 海洋学报, 2020, 42(9): 134-142. [15] MUELLER J L, FARGION G S, MCCLAIN C R, et al. Ocean optics protocols for satellite ocean color sensor validation, Revision 4, Volume VI: Special topics in ocean optics protocols and appendices[M]. Goddard Space Flight Center: Greenbelt, MD, USA, 2003.
[16] GB 17378.4－2007, 海洋监测规范 第4部分: 海水分析[S]. [17] 唐军武, 田国良, 汪小勇, 等. 水体光谱测量与分析Ⅰ: 水面以上测量法[J]. 遥感学报, 2004, 8(1): 37-44. doi: 10.11834/jrs.20040106 [18] 汪小勇, 唐军武, 李铜基, 等. 水面之上法测量水体光谱的关键技术[J]. 海洋技术, 2012, 31(1): 72-76. [19] BAI R F, HE X Q, BAI Y, et al. Atmospheric correction algorithm based on the interpolation of ultraviolet and shortwave infrared bands[J]. Optics Express, 2023, 31(4): 6805-6826. doi: 10.1364/OE.478810
[20] VANHELLEMONT Q, RUDDICK K. Atmospheric correction of metre-scale optical satellite data for inland and coastal water applications[J]. Remote Sensing of Environment, 2018, 216: 586-597. doi: 10.1016/j.rse.2018.07.015
[21] VANHELLEMONT Q, RUDDICK K. Advantages of high quality SWIR bands for ocean colour processing: Examples from Landsat-8[J]. Remote Sensing of Environment, 2015, 161: 89-106. doi: 10.1016/j.rse.2015.02.007
[22] VANHELLEMONT Q. Adaptation of the dark spectrum fitting atmospheric correction for aquatic applications of the Landsat and Sentinel-2 archives[J]. Remote Sensing of Environment, 2019, 225: 175-192. doi: 10.1016/j.rse.2019.03.010
[23] QIU Z F. A simple optical model to estimate suspended particulate matter in Yellow River Estuary[J]. Optics Express, 2013, 21(23): 27891-27904. doi: 10.1364/OE.21.027891
[24] SMAAL A C, SCHELLEKENS T, VAN STRALEN M R, et al. Decrease of the carrying capacity of the Oosterschelde estuary (SW Delta, NL) for bivalve filter feeders due to overgrazing?[J]. Aquaculture, 2013, 404/405: 28-34. doi: 10.1016/j.aquaculture.2013.04.008
[25] NEWELL R I E. Ecosystem influences of natural and cultivated populations of suspension-feeding bivalve molluscs: a review[J]. Journal of Shellfish Research, 2004, 23(1): 51-61.
[26] CARVER C E A, MALLET A L. Estimating the carrying capacity of a coastal inlet for mussel culture[J]. Aquaculture, 1990, 88(1): 39-53. doi: 10.1016/0044-8486(90)90317-G
计量
- 文章访问数: 1325
- HTML全文浏览量: 562
- PDF下载量: 49
