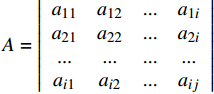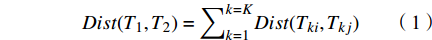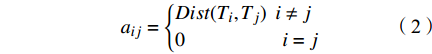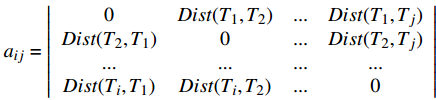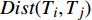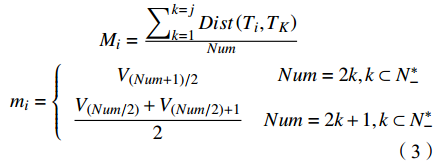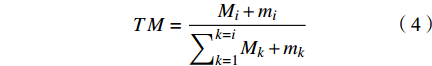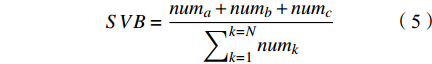A typhoon tracks classification method based on similarity threshold learning
-
摘要:
台风路径分类是分析台风特征的重要途径，同时也是判断台风影响区域和范围的重要方法。目前台风的分类研究主要采用主观识别和K-means聚类等方法，这些方法存在传统聚类算法产生的随机性问题和依赖人工经验设置模型参数的智能化问题，以及针对特定台风研究而导致的局限性问题。针对以上问题，本文提出一种基于相似阈值学习的台风路径分类方法，首先，提出基于密度质心的混合聚类算法，实现了热点区域挖掘，减少了传统方法的随机性；其次，提出基于fastDTW的自适应模体处理算法，实现了更为智能化的路径分类；最后，以登陆湛江的台风路径为例，展示并验证了混合聚类方法的分类效果。
Abstract:The classification of typhoon tracks is an important way to analyze the characteristics of typhoons, and it is also an important method to judge the areas and ranges affected by typhoons. The main methods such as subjective identification and K-means clustering are applied to the research of typhoon classification. These methods have some problems such as randomness caused by traditional clustering algorithms, also rely on artificial experience to set model parameters and are not universal due to specific typhoon research. Aiming at the above problems, this paper proposes a typhoon tracks classification method based on similarity threshold learning. Firstly, a hybrid clustering algorithm based on density center of mass is proposed to realize hot-spot mining and reduce the randomness of traditional methods. Secondly, an adaptive motif processing algorithm based on fastDTW algorithms is proposed to realize more intelligent tracks classification. Finally, the typhoon track landing in Zhanjiang is taken as an example to demonstrate and verify the classification effect of this method.
-
Keywords:
- typhoon disasters /
- similar tracks /
- classification of tracks /
- motif discovery
-
中国位于西北太平洋和南海沿岸，海岸线长约1.8万公里，地理位置十分特殊。据统计，平均每年约20个台风（包括热带低压）可以影响中国沿海，这些台风带来的影响给社会经济造成了极大的损失[1]。为减少台风的负面影响，包括中国在内的世界各国都加大了对台风的监测与研究，其主要热点集中于路径预报、强度预报、风雨预报以及风暴潮预报[2]。
在台风路径的预报中，如何分类引起学者的广泛关注[3-4]，即根据台风路径的空间特征[5]（路径形状、位置等）进行分类，并对分类处理后的台风路径在生命周期、能量、活动季节和登陆概率等方面进行分析。因此，路径分类问题对获取台风特征和预测台风的登陆区域具有重要意义。
传统的台风路径分类，主要采取主观识别法[2]和客观分析法[6-8]。主观识别法主要依靠人工经验，需要研究者有大量的实践经历，但容易产生对专家经验的依赖，并且分类不够准确、稳定；客观分析法中，基于K-means聚类算法[9]的台风路径分类方法具有简单、通用、计算复杂度低、对数据的输入顺序不敏感等优势，受到广泛关注，但也面临算法本身的随机性和不能很好地实现智能化的问题。
Elsner通过K-means聚类算法，仅利用强度最大时的经纬度信息建立参数[6]，将北大西洋台风简单分类为直行路径与北折弯曲路径，此方法没有充分利用各个时次的位置信息。Nakamura在Elsner基础上，进一步以每个定位时次的风速为权重，并将各台风路径的质心和方差作为路径形状和位置特征量，最后将台风分为六类[7]。Camargo等[8]指出，传统K-means聚类算法对台风时间长度的敏感度较低，无法区分不同时间长度的路径，故提出有限混合模型（finite mixture model，FMM）聚类算法。有限混合法将台风路径上各点的经度、纬度时间序列作为独立变量，通过二次多项式回归函数对西北太平洋台风进行分类，因为计算过程复杂，不能将路径间的相似度数值化，并且由于聚类方法本身的特性，故存在一定的随机性。Kowaleski等[10]在前人的基础上提出了回归混合模型，对全球ECMWF、NCEP、CMA和JMA综合预报系统的台风桑迪轨迹和气旋相空间预报进行了聚类。回归混合模型通过贝叶斯信息准则、聚类分配强度和均方预测误差选择最优模型规格，能较好地实现分类，但此模型仅限于特定台风，存在一定的局限性。目前，在台风路径分类的研究中，聚类算法的随机性、人工经验和参数问题的智能化以及研究特定台风而产生的局限性等问题依然存在。
模体挖掘源于数据挖掘思想。模体是指在一组序列中频繁出现且最具有代表性的子序列，该方法具有不需要先验干预和数据自动选择的优势[11-14]。通过模体挖掘方法，本文从一个全新的角度研究和改进台风路径的分类方法。现有的模体挖掘方法依然需要人工设定参数，不能实现自主挖掘模体[15-16]。
本文针对以上问题，提出基于阈值学习的台风路径分类方法。首先，改进传统的K-means聚类算法，提出基于密度质心的混合聚类算法，实现了数据的预处理，取得比传统聚类算法更好的效果；其次，提出了基于fastDTW的自适应模体方法，通过自主阈值学习解决目前存在的依赖先验知识和人工设定参数等问题。
1 材料与方法
1.1 数据
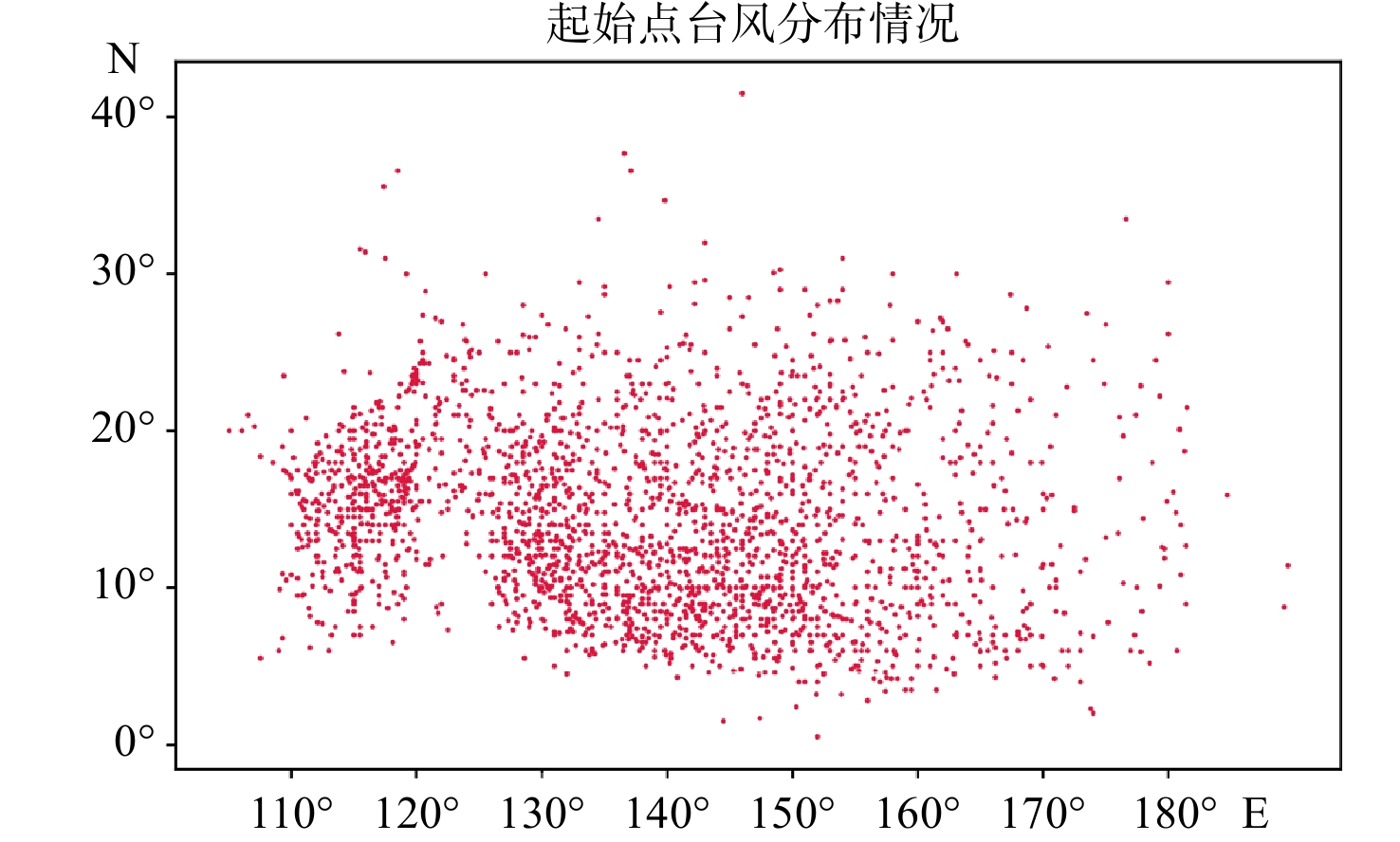
本文数据来自中国气象台公布的1949－2018年台风数据[17]，此数据为CMA台风最佳路径数据集，包含1949－2018年西北太平洋（含南海、赤道以北，东经180°以西）海域台风每6 h的经纬度和强度（图1）。经过整理，本实验以TC编号、每一时刻的经纬度信息、台风最大压强和台风最大风速等作为实验数据。
![]()
图 1 西北太平洋台风起始点分布情况Fig. 1 Distribution of typhoon genesis points over Northwest Pacific1.2 定义
定义1： 设台风路径的观测点P=（Lon，Lat），其中Lon为经度、Lat为纬度，若P为起始点或登陆点，则称P为关键节点；若P为起始点则记P*、为登陆点则记P#。
定义2： 设存在一个集合T={P1，P2，···，Pm}，若T中P1至Pm按时间顺序排列，且代表一条台风的生成到结束所经过的所有观测点，则称T为台风路径，其中m表示此路径观测点的个数。
定义3 ：设一个集合D={P1，P2，···，Pn}，其中P1，P2，···，Pn为关键节点，n表示集合D中关键节点的个数。若集合D中元素全为P*，则称为起始热点区域，记为D*；若元素全为P#，则称为登陆热点区域，记为D#。
定义4 ：设一个关键节点P、常数MinPts以及半径R，若在以P为圆心、R为半径的范围中，节点数量Num（P，R）>MinPts，则称P为核心对象，记为x。
定义5 ：设存在矩阵
$ {A_{}} = \left| {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{...}&{{a_{1i}}}\\ {{a_{21}}}&{{a_{22}}}&{...}&{{a_{2i}}}\\ {...}&{...}&{...}&{...}\\ {{a_{i1}}}&{{a_{i2}}}&{...}&{{a_{ij}}} \end{array}} \right|$ ，若aij为台风Ti与Tj两条路径之间的相似值，则称A为相似矩阵。1.3 基于混合聚类算法的热点区域挖掘
K-means算法在聚类过程中，存在初始中心点的选择具有较高的随机性问题。如果初始中心选择质量较低，则聚类容易陷入局部最佳解而忽略全局[9]，同时也会带来聚类结果的波动。传统K-means算法的随机性将影响台风核心对象的选取，从而影响热点区域挖掘的稳定性，并降低路径分类的精确度。因此，本文针对初始点选择的随机性问题，提出了一种稳定性与代表性俱佳的混合聚类算法，以实现更准确的热点区域挖掘和台风路径分类。
基于混合聚类算法的热点区域挖掘方法是一种基于密度质心的混合聚类算法。混合聚类算法相比传统K-means算法的随机性问题，具有明显的优势。混合聚类有两部分：（1）运用DBSCAN算法[18]密度思想，筛选出n个初始聚类中心{C1，C2，C3，···，Cn}；（2）使用K-means算法，对初始聚类中心进行聚类（如图2所示）。首先，输入所有台风路径的起始点以及登陆点，并形成对应的两类节点集合D*和D#；其次，算法通过轮廓系数[19]来评价聚类效果，并筛选出密度参数（R、MinPts）以及起始点集合D*作为输入，找出核心对象集合X{x1，x2，···，xn}；再次，依次以某一核心对象Pi为出发点，找出由其密度可达的样本生成的聚类簇中心{C1，C2，···，Ck}；最后，将已生成的K个聚类簇为单位，输入K-means算法中，输出各簇类的质心，并以输出各簇类质心为圆点绘制相切圆，最后确定热点区域D。
![]()
图 2 基于混合聚类算法的热点区域挖掘方法流程Fig. 2 Flow chart of hot spot mining method based on hybrid clustering algorithm1.4 基于fastDTW的自适应模体处理
1.4.1 相似矩阵建立
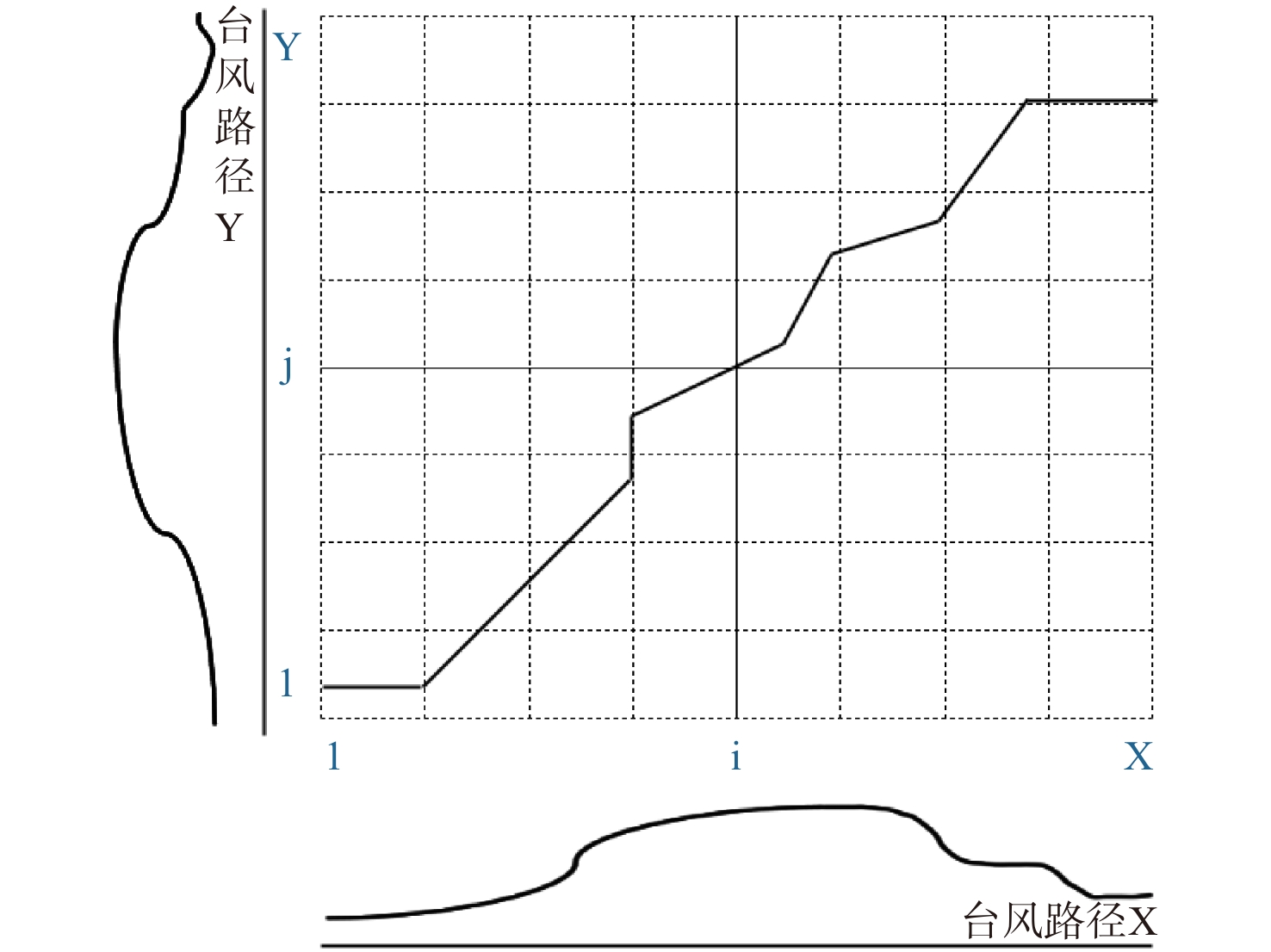
相似矩阵的建立，采用fastDTW方法（fast dynamic time warping，fastDTW）[20]对台风路径进行相似度计算，并将所得结果以矩阵的结构进行存储。fastDTW方法先引入两条长度分别为|X|和|Y|的台风路径T1、T2，再利用距离公式Dist（T1，T2）进行计算：
$$ Dist({T}_{1},{T}_{2})={\sum }_{k=1}^{k=K}Dist({T}_{ki},{T}_{kj}) $$ (1) 如图3和公式（1）所示，将两路径T1、T2平均划分为K段，并结合公式计算出T1、T2两台风路径之间的相似度Dist（T1，T2）。最后，将所有满足热点区域的台风路径依次进行相似计算，并存入相似矩阵A中：
![]()
图 3 fastDTW计算两条台风路径的相似度Fig. 3 fastDTW calculate the similarity between the two typhoon tracks$${a_{ij}} = \left\{ \begin{aligned} & {Dist( {{T_i},{T_j}} )}\;\;{i \ne j}\\& 0\;\;\;\;\qquad\qquad{i = j} \end{aligned}\right.$$ (2) 若有i条路径，则将相似矩阵的aij为：
$${a_{ij}} = \left| {\begin{array}{*{20}{c}} 0&{Dist( {{T_1},{T_2}} )}&{...}&{Dist( {{T_1},{T_j}} )}\\ {Dist( {{T_2},{T_1}} )}&0&{...}&{Dist( {{T_2},{T_j}} )}\\ {...}&{...}&{...}&{...}\\ {Dist( {{T_i},{T_1}} )}&{Dist( {{T_i},{T_2}} )}&{...}&0 \end{array}} \right|$$ 相似矩阵的aij是对应两条台风路径的相似度
$ Dist({T}_{i},{T}_{j}) $ 。同时，相似矩阵A为方阵，且根据公式（2）所示，对角线相似值均为0。1.4.2 路径模体选择
建立相似矩阵，不仅可以直观表示台风路径之间的相似关系，也有助于路径模体的选择。路径模体选择，包括对矩阵的相似值进行排序，计算均值以及中位数，并计算TM指数（track motif index），最终输出路径模体。
$$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{M_i} = \frac{\displaystyle\sum\nolimits_{k = 1}^{k = j} D ist\left( {{T_i},{T_K}} \right)}{{Num}}\\ {m_i} = \left\{ {\begin{array}{*{20}{c}} {{V_{\left( {Num + 1} \right)/2}}}&{Num = 2k,k \subset N_ - ^*}\\ {\dfrac{{{V_{\left( {Num/2} \right)}} + {V_{\left( {Num/2} \right) + 1}}}}{2}}&{Num = 2k + 1,k \subset N_ - ^*} \end{array}} \right. \end{array} $$ (3) 式中：Num为参与相似矩阵运算的台风路径总条数；| V1，V2，···， VNum|是排序后的矩阵第i行的相似值，
$ {N}_{-}^{*} $ 是正整数。则第i行的TM指数：$$ TM=\frac{{M}_{i}+{m}_{i}}{{\displaystyle\sum }_{k=1}^{k=i}{M}_{k}+{m}_{k}} $$ (4) 式中：TM指数越小，则可认定在台风路径集合中，第i条路径出现更为频繁、更具代表性，即路径模体。
1.4.3 相似分布计算
找出路径集合中段路径模体，是解决台风路径分类较为依赖先验知识的关键一步，同时是建立模体资料库的关键一步。本文以路径模体为标准，重新构建一个相似链表L，通过计算台风路径的相似阈值，初步实现台风路径的分类。首先，将链表分为1，2，···，N段，代入计算SVB指数（similar value distribution，SVB）：
$$ SVB=\frac{{{nu}}{{{m}}}_{a}+{{nu}}{{{m}}}_{b}+{{nu}}{{{m}}}_{c}}{{\displaystyle\sum }_{k=1}^{k=N}{{nu}}{{{m}}}_{k}} $$ (5) 式中：a、b、c为对应相似阈值段；numa、numb、numc分别表示根据相似阈值所归属于对应段的台风路径数量。若SVB指数大于80%，则输出a、b、c阈值段以及N值。此时，链表划分为N段所包含的台风路径构成此模体路径下的模体总库，a、b、c所包含的台风路径构成3个模体资料子库。
1.4.4 基于fastDTW的自适应模体处理算法
基于fastDTW的自适应模体处理算法，相对现有的台风分类方法，重点解决了先验知识的问题，同时也解决了机器学习等传统模型参数过多的问题。模体处理通过无人干预、在数据中自主学习相似阈值的方法，找出台风中的路径模体，实现了台风路径分类智能化，为提高台风路径分类的精确度打下基础。
如图4所示，通过fastDTW算法将满足区域条件的台风集合（D）中的各路径依次进行比较，计算其相似性，并保存至相似矩阵；其次，输出对应的相似矩阵Aij；再次，计算对应矩阵每行的均值、中位数，TM指数，输出路径模体；最后，构建相似链表L，计算SVB指数，输出相似值段N，以及子库所需的a、b、c 3个阈值段。
![]()
图 4 基于fastDTW的自适应模体处理算法流程图Fig. 4 Flow chart of adaptive motif processing algorithm based on fastDTW2 结果与讨论
2.1 结果
2.1.1 热点区域处理结果
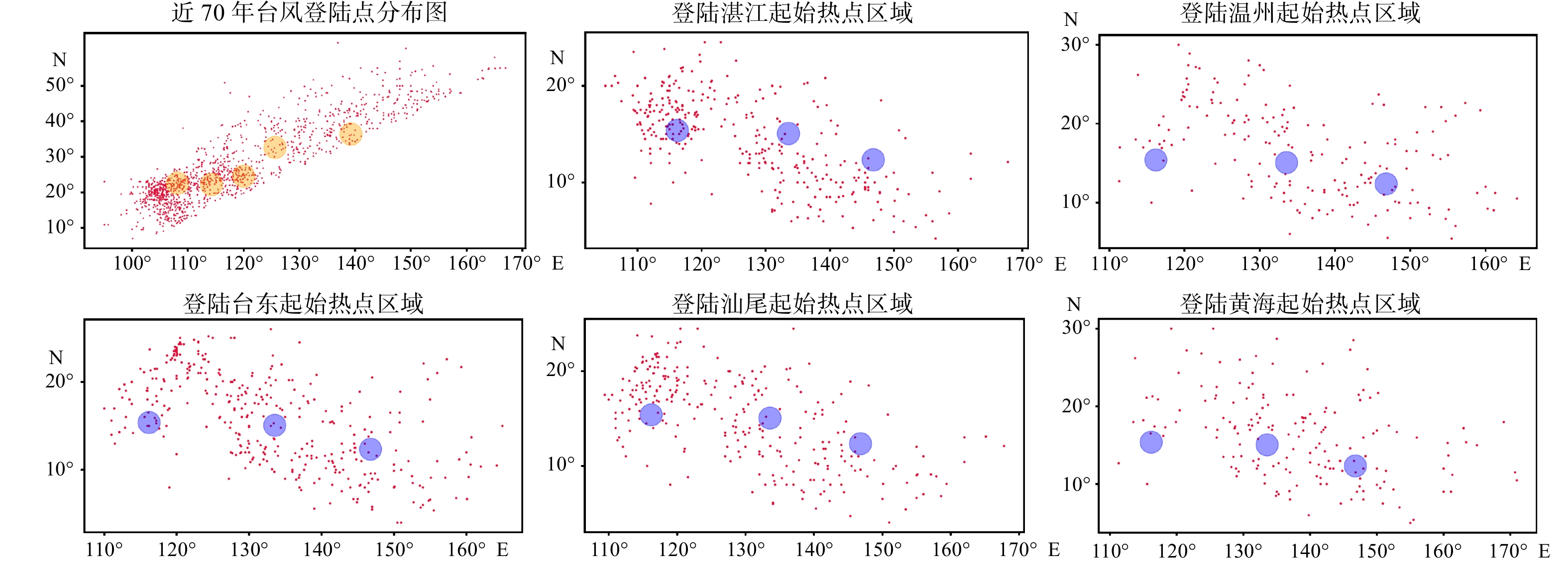
通过基于混合聚类算法的热点区域挖掘方法，本实验以近70年所有台风路径为例，提取台风路径的起始点、登陆点，并利用基于密度质心的混合聚类算法，将其分别进行聚类。如图5所示，实验输出登陆区域共5个，其中黄色圆圈则表示热点登陆区域质心。同时，本次实验主要以登陆中国的台风作为研究样本，结合输出登陆区域结果，将登陆区域确定为湛江区域、汕尾区域、台东区域、温州区域以及黄海区域共5个登陆区域。
轮廓系数[19]为聚类结果质量的评价标准，用于计算聚类簇间的相似度，其取值范围为[−1，1]。若轮廓系数越接近1，则表示聚类效果越好。本实验将起始区域以登陆区域结果为依据，共分成5组数据集，输入参数（R，MinPts），并通过轮廓系数进行结果分析。输出误差分析结果如表1所示，聚类结果如图5所示。
表 1 聚类评价结果对比分析Tab. 1 Comparative analysis of cluster evaluation results算法 R=2 R=3 R=4 R=5 R=6 K-means算法 0.65433 0.5124 0.49177 0.4701 0.40854 DBSCAN算法 0.01261 0.35646 0.23986 0.27828 0.31626 混合聚类算法 0.57232 0.72362 0.62431 0.5923 0.55673 基于以上登陆区域，再次筛选对应登陆区域的台风起始点，再通过混合聚类算法自动筛选出3个起始热点区域。综上，本次实验形成两类热点区域，完成数据预处理过程。
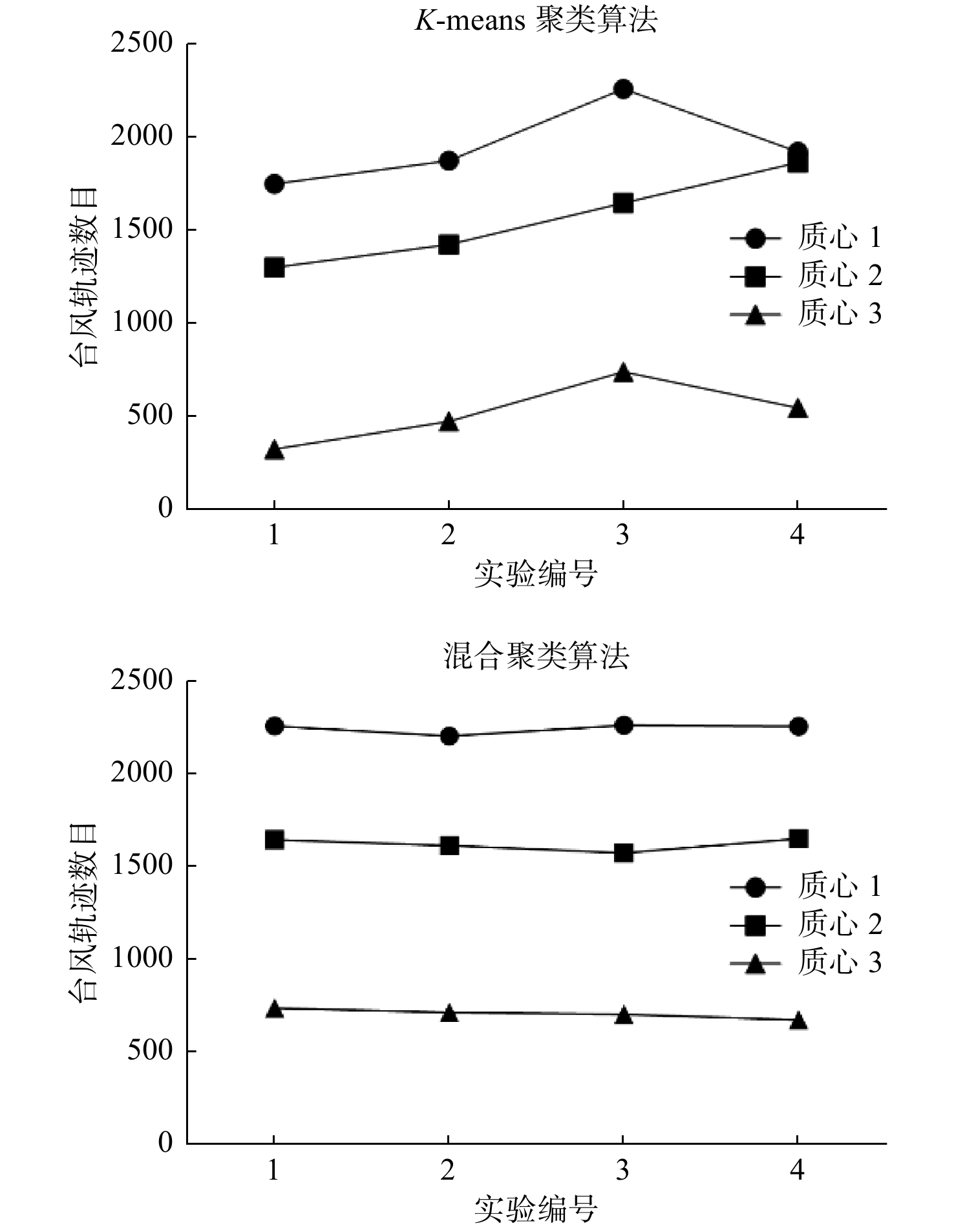
同时，通过与K-means算法进行对比实验，进一步证明了混合聚类算法更为稳定、更具代表性。对比实验共进行4次，并以两种聚类算法输出的区域质心为中心，分别计算满足条件的台风轨迹数目。通过图6可知，混合聚类算法相对于K-means算法，在输出结果上更为稳定，能更好地解决聚类算法的随机性问题。
2.1.2 基于fastDTW的自适应模体处理结果
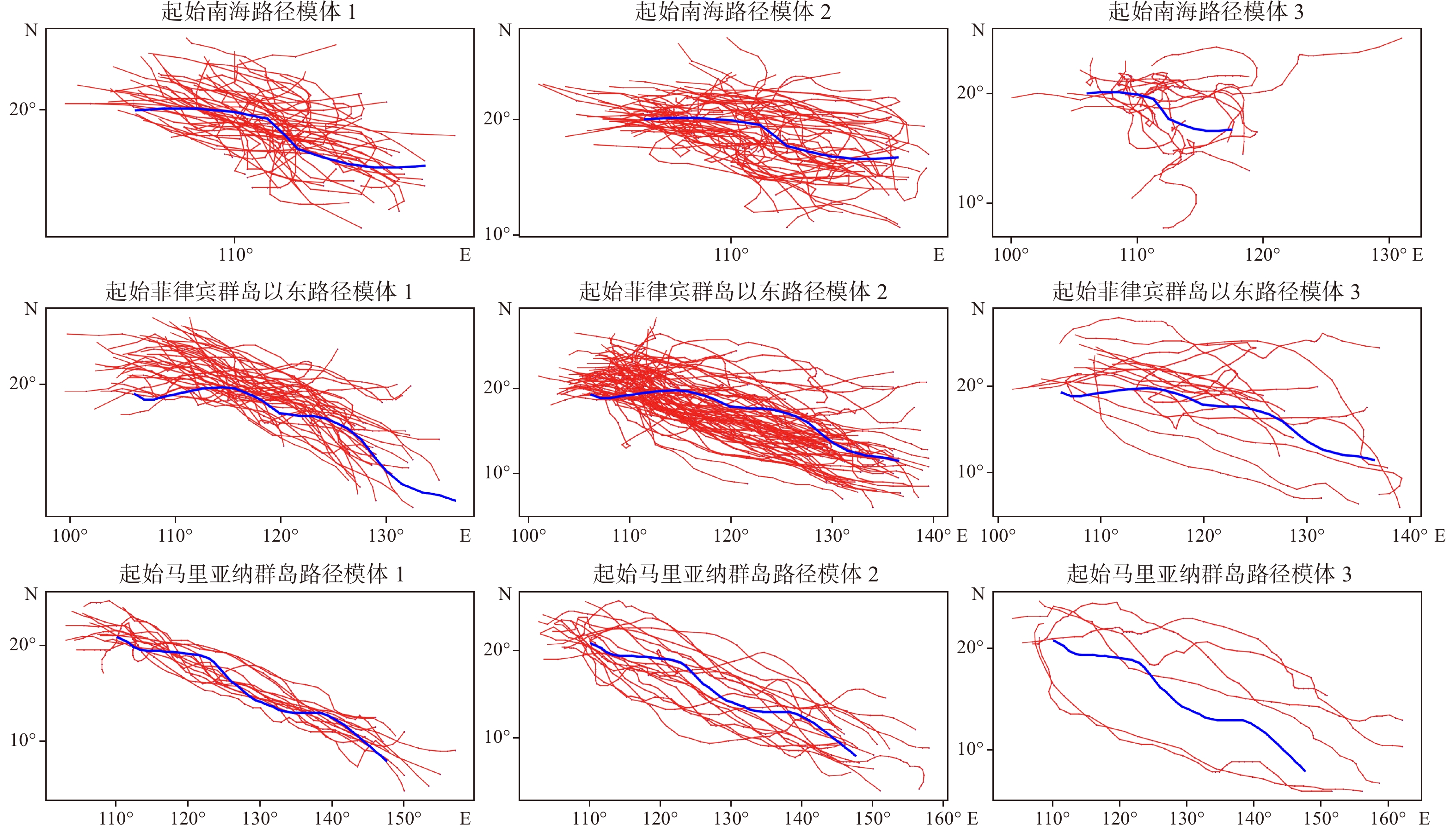
路径模体的选择，是自适应模体处理过程的关键步骤。首先，针对预处理后的路径数据，建立对应的相似矩阵，通过TM指数，选择出此路径集合中的路径模体。本实验以1949－2018年登陆湛江的台风数据来进行自适应模体处理，通过建立相似矩阵，实现了路径模体的选择。
以湛江为例，本文绘制了近70年登陆湛江的台风轨迹路径集合和路径模体（图7）。经过计算，其TM指数分别为0.003522、0.007527、0.017643，即为路径模体。同时，将3条路径分别进行相似分布计算，最终得到N为11，将长度为500的相似链表分为11段，3个阈值段a、b、c分别为0～150、0～150、50～200，SVB指数值分别为95.92%、89.16%、89.47%。
采用上述方法，本文对汕尾、温州、台东以及黄海进行了相同的计算，得到路径模体如图8。
将本文的实验结果与传统K-means聚类方法分类的结果比较可知，基于fastDTW的自适应模体处理方法可以将起始南海区域的台风进一步划分成5类，具有一定的创新性和代表性。本文的算法将传统的西移、转向台风路径从不同的起始区域和登陆区域进行细化。
2.2 讨论
2.2.1 台风路径可视化和数据库领域应用
2.1.2节路径模体以及相似阈值学习的结果，可以用于模体资料库的构建。如图9所示，以相似段值N=11为子类，进一步数值化路径相似分布，构建模体资料库对应的子资料库。
![]()
图 9 以登陆湛江的路径模体为标准，根据相似阈值划分出的台风路径模体子资料库Fig. 9 Taking the landing path motif of Zhanjiang as the standard, the sub database of typhoon path motifs were classified according to the similarity threshold图9分别绘制了南海区域登陆湛江的3个台风模体子资料库，其相似分布分别为0～50、50～100、100～150；在菲律宾东部区域登陆湛江的3个台风模体子资料库，分别为0～50、50～100、100～150；在群岛区域登陆湛江的3个台风模体子资料库，分别为50～100、100～150、150～200。
由图9可知，历史台风路径的相似阈值越接近，则地理位置和路径形状都越接近，这充分证明了基于相似阈值学习的台风路径分类方法，能很好地应用于未来模体资料库的建立。因此，该方法对台风路径的可视化和台风数据库的建设有一定的指导意义。
2.2.2 台风灾害分析领域应用
通过九类路径模体资料库压强变化的分析，进一步证实了基于相似阈值学习的台风路径分类算法在台风灾害分析领域的应用价值。
图10从左至右分别表示起始南海、菲律宾以东、各群岛区域并登陆湛江的台风（图7）子库的压强变化与分布情况。由图10可知，起始南海的路径模体资料库中3类子库的压强分布以及变化趋势基本一致。其中，子库一台风的生命周期较短，普遍为96 h，且于48 h时压强达到最小值；子库二台风的生命周期适中，普遍为150 h，且于90 h时压强达到最小值；子库三台风的生命周期较长，普遍为210 h，且于132 h时压强达到最小值。
![]()
图 10 九类路径模体资料子库中单条台风压强变化趋势以及各子库中路径压强总体分布情况Fig. 10 The pressure variation trend of a single typhoon in the nine classpath model subdatabase and the overall distribution of the path pressure in each subdatabase通过本文的路径模体资料库可以发现，各子资料库的压强分布以及变化趋势具有明显的规律性，能很好地体现基于阈值学习的台风路径分类方法的正确性。本实验虽然没有直接以压强等相关物理量参与分类，但是分类后的台风路径中，其物理量却有相当明显的差异。
3 结 论
（1）通过热点区域处理，确定了台风路径起始、登陆的热点区域，解决了传统聚类的随机性问题，实现了更加精确与直观的聚类效果，并与现有研究进行对比，证明了此方法的正确性以及实用性。
（2）以登陆湛江区域的台风为例，通过fastDTW自适应模体处理方法挖掘出TM指数分别为0.003522、0.007527、0.017643的台风路径模体，计算后的SVB指数分别为95.92%、89.16%、89.47%，通过模体资料库分析可知，混合聚类方法具有一定的应用价值。
（3）将台风路径进行分类并验证，结合台风路径可视化以及台风数据库的建设等领域，实现了台风路径分类的数值化、智能化，为探索台风路径的可视化与台风登陆区域的灾害分析提供了研究思路。
-
![]()
图 1 西北太平洋台风起始点分布情况
Fig. 1. Distribution of typhoon genesis points over Northwest Pacific
![]()
图 2 基于混合聚类算法的热点区域挖掘方法流程
Fig. 2. Flow chart of hot spot mining method based on hybrid clustering algorithm
![]()
图 3 fastDTW计算两条台风路径的相似度
Fig. 3. fastDTW calculate the similarity between the two typhoon tracks
![]()
图 4 基于fastDTW的自适应模体处理算法流程图
Fig. 4. Flow chart of adaptive motif processing algorithm based on fastDTW
![]()
图 9 以登陆湛江的路径模体为标准，根据相似阈值划分出的台风路径模体子资料库
Fig. 9. Taking the landing path motif of Zhanjiang as the standard, the sub database of typhoon path motifs were classified according to the similarity threshold
![]()
图 10 九类路径模体资料子库中单条台风压强变化趋势以及各子库中路径压强总体分布情况
Fig. 10. The pressure variation trend of a single typhoon in the nine classpath model subdatabase and the overall distribution of the path pressure in each subdatabase
表 1 聚类评价结果对比分析
Tab. 1 Comparative analysis of cluster evaluation results
算法 R=2 R=3 R=4 R=5 R=6 K-means算法 0.65433 0.5124 0.49177 0.4701 0.40854 DBSCAN算法 0.01261 0.35646 0.23986 0.27828 0.31626 混合聚类算法 0.57232 0.72362 0.62431 0.5923 0.55673 
下载: 导出CSV
-
[1] REN R, YU D Q, WANG L X, et al. Typhoon triggered operation tunnel debris flow disaster in coastal areas of SE China[J]. Geomatics, Natural Hazards and Risk, 2019, 10(1): 562-575. doi: 10.1080/19475705.2018.1535452
[2] 陈联寿, 端义宏, 宋丽莉, 等. 台风预报及其灾害[M]. 北京: 气象出版社, 2012. [3] MENG Y, LU J, LIAO Q L. Analysis of the characteristics of west-pacific typhoons affecting the sea area around the island of Taiwan[J]. Journal of Tropical Meteorology, 2005, 11(2): 222-223.
[4] 秦丽娟, 董 庆, 薛存金. 西北太平洋热带气旋源地30 a的季节和年代际变化[J]. 海洋环境科学, 2015, 34(5): 723-728. [5] 王 毅, 石汉青, 黄思训. 西北太平洋热带气旋的时空分布特征分析[J]. 自然灾害学报, 2009, 18(6): 166-174. doi: 10.3969/j.issn.1004-4574.2009.06.028 [6] ELSNER J B. Tracking hurricanes[J]. Bulletin of the American Meteorological Society, 2003, 84(3): 353-356. doi: 10.1175/BAMS-84-3-353
[7] NAKAMURA J, LALL U, KUSHNIR Y, et al. Classifying north Atlantic tropical cyclone tracks by mass moments[J]. Journal of Climate, 2009, 22(20): 5481-5494. doi: 10.1175/2009JCLI2828.1
[8] CAMARGO S J, ROBERTSON A W, GAFFNEY S J, et al. Cluster analysis of typhoon tracks. Part II: Large-scale circulation and ENSO[J]. Journal of Climate, 2007, 20(14): 3654-3676. doi: 10.1175/JCLI4203.1
[9] 伍育红. 聚类算法综述[J]. 计算机科学, 2015, 42(S1): 491-499, 524. [10] KOWALESKI A M, EVANS J L. Regression mixture model clustering of multimodel ensemble forecasts of hurricane sandy: partition characteristics[J]. Monthly Weather Review, 2016, 144(10): 3825-3846. doi: 10.1175/MWR-D-16-0099.1
[11] LIN J, KEOGH E, WEI L, et al. Experiencing SAX: a novel symbolic representation of time series[J]. Data Mining and Knowledge Discovery, 2007, 15(2): 107-144. doi: 10.1007/s10618-007-0064-z
[12] CHIU B, KEOGH E, LONARDI S. Probabilistic discovery of time series motifs[C]//Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Washington: ACM, 2003: 493-498.
[13] MUEEN A, KEOGH E, ZHU Q, et al. Exact discovery of time series motifs[C]//Proceedings of the 2009 SIAM International Conference on Data Mining. Sparks: Society for Industrial and Applied Mathematics, 2009: 473-484.
[14] LI Y, LIN J, OATES T. Visualizing variable-length time series motifs[C]//Proceedings of the 2012 SIAM International Conference on Data Mining. Sparks: Society for Industrial and Applied Mathematics, 2012: 895-906.
[15] GAO Y F, LIN J, RANGWALA H. Iterative grammar-based framework for discovering variable-length time series motifs[C]//Proceedings of 2016 15th IEEE International Conference on Machine Learning and Applications. Anaheim: IEEE, 2016: 111-116.
[16] YEH C C M, ZHU Y, ULANOVA L, et al. Time series joins, motifs, discords and shapelets: a unifying view that exploits the matrix profile[J]. Data Mining and Knowledge Discovery, 2018, 32(1): 83-123. doi: 10.1007/s10618-017-0519-9
[17] YING M, ZHANG W, YU H, et al. An overview of the china meteorological administration tropical cyclone database[J]. Journal of Atmospheric and Oceanic Technology, 2014, 31(2): 287-301. doi: 10.1175/JTECH-D-12-00119.1
[18] KUMAR K M, REDDY A R M. A fast DBSCAN clustering algorithm by accelerating neighbor searching using Groups method[J]. Pattern Recognition, 2016, 58: 39-48. doi: 10.1016/j.patcog.2016.03.008
[19] 朱连江, 马炳先, 赵学泉. 基于轮廓系数的聚类有效性分析[J]. 计算机应用, 2010, 30(S2): 139-141. [20] LOHRER J, LIENKAMP M. Building representative velocity profiles using FastDTW and spectral clustering[C]//Proceedings of 201514th International Conference on its Telecommunications. Copenhagen: IEEE, 2015: 45-49.
-
期刊类型引用(2)
1. 孙峤，黄家凯，郭凌旭，马世乾，夏昊天，刘荣浩，王梓博，乔骥. 强风雨天气等极端灾害下的配电网弹性提升优化策略. 电网与清洁能源. 2024(11): 86-96 . 
百度学术
2. 李颖，金茹，许娈，林青，姜瑜君. 基于路径与环境场最优赋权的致灾相似台风检索方法研究. 水利水电技术(中英文). 2023(07): 14-26 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 1059
- HTML全文浏览量: 457
- PDF下载量: 58
- 被引次数: 2
